Interseção de reta e circunferências

Uma forma de encontrar a posição relativa entre uma reta e uma circunferência é verificando a sua intersecção, ou seja, analisando se a reta e a circunferência terão dois pontos em comum, apenas um ponto em comum ou nenhum ponto em comum.

O valor dessa intersecção é a solução do sistema formado com a equação geral da reta e com a equação reduzida da circunferência. Considerando a equação geral da reta ax+by+c = 0 e a equação reduzida da circunferência (x - a)² + (y - b)² = R².

Resolvendo o sistema é possível encontrar uma equação do segundo grau, analisando o seu descriminante Δ é possível determinar a posição da reta em relação à circunferência:

Δ > 0 reta secante à circunferência
Δ = 0 reta tangente à circunferência
Δ < 0 reta externa à circunferência.

Se o discriminante Δ for maior ou igual à zero, para descobrir as coordenadas dos pontos é preciso terminar a resolução da equação do segundo grau.

Exemplo: Verifique se a circunferência (x+1)² + y² = 25 e a reta x + y – 6 = 0 possui algum ponto de intersecção.

Resolução:

x + y – 6 = 0 → equação 1
(x+1)² + y² = 25 → equação 2

Escolhemos uma das duas equações e isolamos uma das incógnitas.

x + y – 6 = 0
x = 6 – y

Substituímos o valor de x na equação 2.

(6 – y +1)² + y² = 25
(-y + 7)² + y² = 25
(-y)² – 14y + 49 + y² = 25
y² – 14y + 49 – 25 + y² = 0
2y² – 14y + 24 = 0 (: 2)
y² – 7y + 12 = 0

Δ = b² – 4ac
Δ = (-7)² – 4 . 1 . 12
Δ = 49 – 48
Δ = 1

Como o descriminante Δ é maior que zero sabemos que essa reta é secante à circunferência, agora para descobrir o valor das coordenadas dos dois pontos pertencentes à circunferência é preciso terminar de resolver a equação.


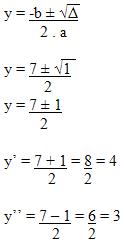
Para y’= 4
x = 6 – y
x = 6 – 4
x = 2

Para y’’ = 3
x = 6 – y
x = 6 – 3
x = 3

Portanto, os dois pontos que interceptam a circunferência são: (2,4) e (3,3).
www.mundoeducacao.com.br