Posição relativa entre duas circunferências

No estudo analítico da circunferência, os elementos raio, diâmetro e centro da circunferência são fundamentais para conclusões de diversos problemas e para a determinação da equação que define essa forma geométrica tão importante. Em se tratando de posições relativas entre duas circunferências, elas podem ser: tangentes, secantes, externas, internas ou concêntricas. Vamos analisar cada caso.
1. Circunferências tangentes.

a) Tangentes externas
Duas circunferências são tangentes internas quando possuem somente um ponto em comum e uma exterior à outra. A condição para que isso ocorra é que a distância entre os centros das duas circunferências seja equivalente à soma das medidas de seus raios.

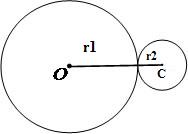
d_OC = r₁ + r₂

b) Tangentes internas
Duas circunferências são tangentes internas quando possuem apenas um ponto em comum e uma esteja no interior da outra. A condição para que isso ocorra é que a distância entre os dois centros seja igual à diferença entre os dois raios.

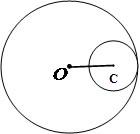
d_OC = r₁ - r₂

2. Circunferências externas.
Duas circunferências são consideradas externas quando não possuem pontos em comum. A condição para que isso ocorra é que a distância entre os centros das circunferências deve ser maior que a soma das medidas de seus raios.

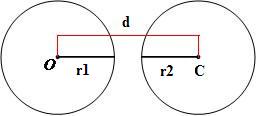
d_OC > r₁ + r₂

3. Circunferências secantes.
Duas circunferências são consideradas secantes quando possuem dois pontos em comum. A condição para que isso aconteça é que a distância entre os centros das circunferências deve ser menor que a soma das medidas de seus raios.

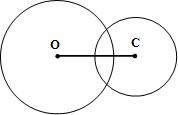
d_CO < r₁ + r₂

4. Circunferências internas.
Duas circunferências são consideradas internas quando não possuem pontos em comum e uma está localizada no interior da outra. A condição para que isso ocorra é que a distância entre os centros das circunferências deve ser equivalente à diferença entre as medidas de seus raios.

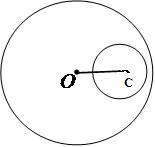
d_OC < r₁ - r₂

5. Circunferências concêntricas.
Duas circunferências são consideradas concêntricas quando possuem o centro em comum. Nesse caso, a distância entre os centro é nula.

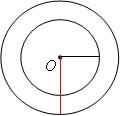
d_CO = 0

Exemplo: Dadas as circunferências λ e σ, de equações:
λ: x² + y² = 9
σ: (x – 7)² + y² = 16
Verifique a posição relativa entre elas.

Solução: Para resolução do problema devemos saber as coordenadas do centro e a medida do raio de cada uma das circunferências. Através da equação de cada uma podemos encontrar esses valores.
Como a equação de toda circunferência é da forma: (x – x₀)² + (y – y₀)² = r², teremos:

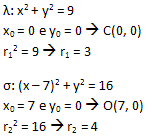
Conhecidos os elementos de cada uma das circunferências, vamos calcular a distância entre os centros, utilizando a fórmula da distância entre dois pontos.

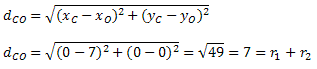
Por Marcelo Rigonatto
Especialista em Estatística e Modelagem Matemática