Pular para o conteúdo principal

Pirâmides

Por
Dada uma região poligonal de n vértices e um ponto V fora da região (outro plano), ao traçarmos segmentos de retas entre os vértices da região poligonal e o ponto V, construímos uma pirâmide que será classificada de acordo com o número de lados do polígono da base.

Os segmentos AV, BV e CV são as arestas laterais da pirâmide.
Os pontos A, B, C e V são os vértices.
Os triângulos VAB,VBC e VCA são as faces laterais.
O triângulo ABC é outra face da pirâmide e constitui a base.
A distância do ponto V ao centro da base constitui a altura da pirâmide.

A classificação de uma pirâmide depende do número de arestas da região da área da base.

Base é um triângulo
Nome: pirâmide triangular
Número de faces: três faces laterais mais face da base, portanto, quatro faces.

Base é um quadrado
Nome: pirâmide quadrangular
Número de faces: quatro faces laterais mais face da base, portanto, cinco faces.

Base é um pentágono
Nome: pirâmide pentagonal
Número de faces: cinco faces laterais mais face da base, portanto, seis faces.

Base é um hexágono
Nome: pirâmide de base hexagonal
Número de faces: seis faces laterais mais face da base, portanto, sete faces.


Pirâmide triangular Pirâmide quadrangular Pirâmide pentagonal



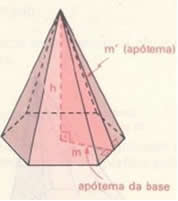
Altura, apótema da base e apótema da pirâmide

h: altura da pirâmide
m’: apótema da pirâmide
m: apótema da base

Pelo teorema de Pitágoras temos:
m’² = h² + m²




Área da base

A área da base de uma pirâmide depende da área do polígono em questão, sendo calculada pela expressão:

onde P: perímetro do polígono e a: apótema do polígono.


Área lateral
É a soma de todas as áreas laterais.

Área totalSoma da área lateral com a área da base.
At = Al + Ab


Volume

O volume de uma pirâmide é dado pela expressão:

onde Ab: área da base (depende do polígono) e h: altura da pirâmide.


Planificação de uma pirâmide

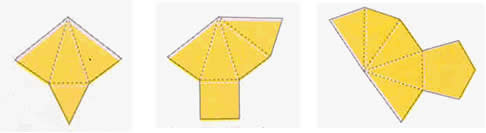
Pirâmide triangular Pirâmide quadrangular Pirâmide pentagonal

Marcos Noé
Marcadores:

Comentários

Postar um comentário

Postagens mais visitadas deste blog

EQUAÇÃO DE 1° GRAU

Por
EQUAÇÃO DE 1° GRAU SENTENÇAS Uma sentença matemática pode ser verdadeira ou falsa exemplo de uma sentença verdadeira a) 15 + 10 = 25 b) 2 . 5 = 10 exemplo de uma sentença falsa a) 10 + 3 = 18 b) 3 . 7 = 20 SENTEÇAS ABERTAS E SENTENÇAS FECHADAS Sentenças abertas são aquelas que possuem elementos desconhecidos. Esses elementos desconhecidos são chamados variáveis ou incógnitas. exemplos a) x + 4 = 9 (a variável é x) b) x + y = 20 (as variáveis são x e y) Sentenças fechada ou são aquelas que não possuem variáveis ou incógnitas. a) 15 -5 = 10 (verdadeira) b) 8 + 1 = 12 (falsa) EQUAÇÕES Equações são sentenças matemáticas abertas que apresentam o sinal de igualdade exemplos a) x - 3 = 13 ( a variável ou incógnita x) b) 3y + 7 = 15 ( A variável ou incógnita é y) A expressão à esquerdas do sinal = chama-se 1º membro A expressão à direita do sinal do igual = chama-se 2º membro RESOLUÇÃO DE EQUAÇÕES DO 1º GRAU COM UMA VARIÁVEL O processo de res
45 comentários
Leia mais

VALOR NÚMERICO DE UMA EXPRESSÃO ALGÉBRICA

Por
Para obter o valor numérico de uma expressão algébrica, você deve proceder do seguinte modo: 1º Substituir as letras por números reais dados. 2º Efetuar as operações indicadas, devendo obedecer à seguinte ordem: a) Potenciação b) Divisão e multiplicação c) Adição e subtração IMPORTANTE! Convém utilizar parênteses quando substituímos letras por números negativos Exemplo 1 Calcular o valor numérica de 2x + 3a para x = 5 e a = -4 2.x+ 3.a 2 . 5 + 3 . (-4) 10 + (-12) -2 Exemplo 2 Calcular o valor numérico de x² - 7x +y para x = 5 e y = -1 x² - 7x + y 5² - 7 . 5 + (-1) 25 – 35 -1 -10 – 1 -11 Exemplo 3 Calcular o valor numérico de : 2 a + m / a + m ( para a = -1 e m = 3) 2. (-1) + 3 / (-1) + 3 -2 + 3 / -1 +3 ½ Exemplo 4 Calcular o valor numérico de 7 + a – b (para a= 2/3 e b= -1/2 ) 7 + a – b 7 + 2/3 – (-1/2) 7 + 2/3 + 1 / 2 42/6 + 4/6 + 3/6 49/6 EXERCICIOS 1) Calcule o valor numérico das expressões: a) x – y (para x =5 e y = -4) (R:
57 comentários
Leia mais

OPERAÇÕES COM RADICAIS

Por
RADICAIS SEMELHANTES Radicais semelhantes são os que têm o mesmo índice e o mesmo radicando Exemplos de radicais semelhantes a) 7√5 e -2√5 b) 5³√2 e 4³√2 Exemplos de radicais não semelhantes a) 5√6 e 2√3 b) 4³√7 e 5√7 ADIÇÃO E SUBTRAÇÃO 1º CASO : Os radicais não são semelhantes Devemos proceder do seguinte modo: a) Extrair as raízes (exatas ou aproximadas) b) Somar ou subtrair os resultados Exemplos 1) √16 + √9 = 4 + 3 = 7 2) √49 - √25 = 7 – 5 = 2 3) √2 + √3 = 1,41 + 1,73 = 3,14 Neste último exemplo, o resultado obtido é aproximado, pois √2 e √3 são números irracionais (representação decimal infinita e não periódica) EXERCÍCIOS 1) Calcule a) √9 + √4 = 5 b) √25 - √16 = 1 c) √49 + √16 = 11 d) √100 - √36 = 4 e) √4 - √1 = 1 f) √25 - ³√8 = 3 g) ³√27 + ⁴√16 = 5 h) ³√125 - ³√8 = 3 i) √25 - √4 + √16 = 7 j) √49 + √25 - ³√64 = 8 2º CASO : Os radicais são semelhantes. Para adicionar ou subtrair radicais semelhantes, procedemos como na redução de
66 comentários
Leia mais