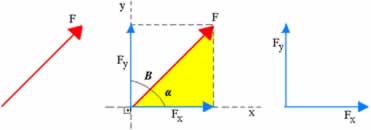
Decomposição de forças em duas componentes perpendiculares Fx e Fy
Há situações em que pode ser vantajoso substituir uma força .jpg) por duas outras forças perpendiculares, isto é, fazer a decomposição de
por duas outras forças perpendiculares, isto é, fazer a decomposição de .jpg) em forças componentes perpendiculares, como fazemos quando trabalhamos com vetores em geral.
em forças componentes perpendiculares, como fazemos quando trabalhamos com vetores em geral.
.jpg) por duas outras forças perpendiculares, isto é, fazer a decomposição de
por duas outras forças perpendiculares, isto é, fazer a decomposição de .jpg) em forças componentes perpendiculares, como fazemos quando trabalhamos com vetores em geral.
em forças componentes perpendiculares, como fazemos quando trabalhamos com vetores em geral.
Vejamos, por exemplo, o caso da força .jpg) da figura acima. Vamos decompor essa força em duas forças componentes sobre as direções perpendiculares x e y. Dessa forma, podemos afirmar que:
da figura acima. Vamos decompor essa força em duas forças componentes sobre as direções perpendiculares x e y. Dessa forma, podemos afirmar que:
.jpg) da figura acima. Vamos decompor essa força em duas forças componentes sobre as direções perpendiculares x e y. Dessa forma, podemos afirmar que:
da figura acima. Vamos decompor essa força em duas forças componentes sobre as direções perpendiculares x e y. Dessa forma, podemos afirmar que: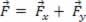
Isto é, a força 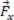 é a resultante de
é a resultante de 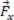 e
e 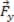 . Isso significa que as forças
. Isso significa que as forças 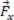 e
e 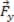 , atuando juntas, produzem o mesmo efeito de força
, atuando juntas, produzem o mesmo efeito de força .jpg) atuando sozinha. Portanto, a força
atuando sozinha. Portanto, a força .jpg) da figura acima pode ser substituída pelo par de forças
da figura acima pode ser substituída pelo par de forças 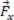 e
e 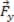 .
.
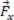 é a resultante de
é a resultante de 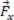 e
e 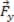 . Isso significa que as forças
. Isso significa que as forças 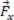 e
e 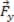 , atuando juntas, produzem o mesmo efeito de força
, atuando juntas, produzem o mesmo efeito de força .jpg) atuando sozinha. Portanto, a força
atuando sozinha. Portanto, a força .jpg) da figura acima pode ser substituída pelo par de forças
da figura acima pode ser substituída pelo par de forças 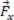 e
e 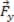 .
.
Vamos considerar o triângulo retângulo em amarelo da figura acima. A partir dele temos que:
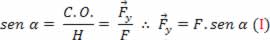
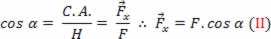
Se considerarmos o triângulo retângulo não colorido da figura acima, teremos a seguinte relação:
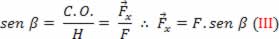

Lembrando sempre que:
- Sendo α e β complementares (α + β = 90º), temos:
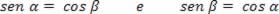
Domiciano Correa Marques da Silva em Mecânica
Nenhum comentário:
Postar um comentário