Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
O agrupamento de termos com características semelhantes é uma definição para a palavra conjunto. Os conjuntos recebem nomes de acordo com a quantidade de elementos que podem vir a ser agrupados.
Conjunto finito
Esse tipo de conjunto representa uma quantidade limitada de elementos. Por exemplo, o conjunto dos números compreendidos entre 1 e 10 será representado da seguinte maneira: {x / 1 < x < 10} ou {2, 3, 4, 5, 6, 7, 8, 9}
Conjunto infinito
Apresenta uma quantidade infinita (ilimitada de termos). Por exemplo:
O conjunto dos reais é considerado um conjunto infinito, pois não possui fim.
O conjunto dos números inteiros também é considerado infinito.
Conjunto unitário
Esse conjunto é caracterizado por possuir apenas um único elemento. Por exemplo:
O conjunto dos números naturais compreendidos entre 0 e 2. Nesse caso existe somente um elemento, o 1. Representamos por {1}.
O conjunto dos números inteiros compreendidos entre –3 e –1. Entre os números –3 e –1 existe apenas o número inteiro –2. Portanto, a representação deste conjunto unitário é {–2}.
Conjunto Vazio
O conjunto vazio não possui nenhum elemento, a sua representação pode ser feita utilizando duas simbologias: { } ou Ø. Por exemplo:
O conjunto dos números naturais antecessores ao 0 (zero) é considerado vazio, pois nos números naturais não existe antecessor de zero.
O conjunto dos números fracionários existentes no conjunto dos números inteiros é considerado um conjunto vazio, pois não existem frações dentre os números inteiros.
Conjunto Universo
É o conjunto representativo de todos os elementos da conjuntura na qual estamos trabalhando, e também de todos os conjuntos relacionados. Na representação do conjunto universo utilizamos a letra maiúscula U.
A Teoria dos Conjuntos foi criada e desenvolvida pelo Matemático russo George Cantor (1845-1918), trata-se do estudo das propriedades dos conjuntos, relações entre conjuntos e relações entre os elementos e o próprio conjunto.
Ao trabalharmos com conjuntos usamos símbolos matemáticos capazes de demonstrar determinadas situações entre conjuntos e elementos. Se temos um elemento p pertencente ao conjunto P podemos dizer que p pertence a P, ou p Є P.
Caso o elemento não pertença ao conjunto, podemos utilizar a seguinte notação:
(p não pertence a P).
Um conjunto pode possuir subconjuntos, se todos os elementos do conjunto A pertencem ao conjunto B podemos dizer que A é subconjunto de B.
Qualquer conjunto possui como subconjunto um conjunto vazio representado por { } ou Ø.
A união de dois ou mais conjuntos constitui um novo conjunto com todos os elementos dos outros dois.
A intersecção entre dois ou mais conjuntos constitui um conjunto que contém simultaneamente os elementos de dois ou mais conjuntos.
A diferença entre dois conjuntos A e B tem como resultado um conjunto com os elementos de A que não pertencem a B.
Dados dois conjuntos A e B, a relação existente entre os elementos do conjunto A com os elementos do conjunto B receberá o nome de função. Notação f: A→B. Observe:
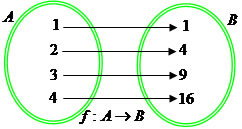
Note que para cada elemento do conjunto A existe um elemento no conjunto B, essa relação pode ser definida pela seguinte lei de formação f(x) = x2.
A
|
B
|
x
|
f(x) = x2
|
1
|
f(1) = 12 = 1
|
2
|
f(2) = 22 = 4
|
3
|
f(3) = 32 = 9
|
4
|
f(4) = 42 = 16
|
IntersecçãoA intersecção de A com B é o conjunto formado pelos elementos comuns a A e B.
Notação A ∩ B.
A ∩ B = {x / x Є A e x Є B}
União
A união de A com B é o conjunto formado por todos os elementos pertencentes a A ou a B.
Notação A U B.
A U B = {x / x Є A e x Є B}
Diferença
A diferença entre A e B é o conjunto formado pelos elementos que pertencem a A e não pertencem a B.
Notação A – B.
A – B = {x / x Є A e x B}
Exemplo 1
Sendo A = {1, 2, 3, 4} e B = {2, 4, 6}
A ∩ B = {2, 4}
A U B = {1, 2, 3, 4, 6}
A – B = {1, 3}
B – A = {6}
Exemplo 2
Sendo A = {1, 2, 3, 4, 5, 6, 7, 8, 9} e B = {10, 11, 12, 13, 14, 15}
A ∩ B = Ø (conjunto vazio)
A U B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}
A – B = {1, 2, 3, 4, 5, 6, 7, 8, 9}
B – A = {10, 11, 12, 13, 14, 15}
Quando falamos de operação lembramos logo de adição, subtração, divisão, multiplicação entre números. É possível também operar conjuntos.
Essas operações recebem nomes diferentes, como: União de conjuntos, Intersecção de conjuntos, Diferença de conjunto, Conjunto complementar.
Todas essas operações são representadas por símbolos diferentes, veja a representação de cada uma delas.
► União de conjuntos
Dado dois conjuntos A = {1, 2, 3, 4, 5} e B = {6, 7}, a união deles seria pegar todos os elementos de A e de B e unir em apenas um conjunto (sem repetir os elementos comuns). O conjunto que irá representar essa união ficará assim: {1, 2, 3, 4, 5, 6, 7}.
A representação da união de conjuntos é feita pelo símbolo U. Então,
A U B = {1, 2, 3, 4, 5, 6, 7}.
►Intersecção de conjuntos
Quando queremos a intersecção de dois conjuntos é o mesmo que dizer que queremos os elementos que eles têm em comum.
Dado dois conjuntos A = {1, 2, 3, 4, 5, 6} e B = {5, 6, 7}, a intersecção é representada pelo símbolo ∩, então A ∩ B = {5, 6}, pois 5 e 6 são elementos que pertencem aos dois conjuntos.
Se dois conjuntos não tem nenhum elemento comum a intersecção deles será um conjunto vazio.
Dentro da interseção de conjuntos há algumas propriedades:
1) A intersecção de um conjunto por ele mesmo é o próprio conjunto: A ∩ A = A
2) A propriedade comutatividade na intersecção de dois conjuntos é:
A ∩ B = B ∩ A.
3) A propriedade associativa na intersecção de conjuntos é:
A ∩ (B ∩ C) = (A ∩ B) ∩ C
► Diferença entre conjunto
Dado o conjunto A = {0, 1, 2, 3, 4, 5} e o conjunto B = {5, 6, 7} a diferença desses conjuntos é representada por outro conjunto, chamado de conjunto diferença.
Então A – B serão os elementos do conjunto A menos os elementos que pertencerem ao conjunto B.
Portanto A – B = {0, 1, 2, 3, 4}.
►Conjunto complementar
Conjunto complementar está relacionado com a diferença de conjunto.
Achamos um conjunto complementar quando, por exemplo, dado um conjunto A e B e o conjunto B A, então B é complementar em relação a A.
A = {2, 3, 5, 6, 8}
B = {6,8}
B
Quando se trata de conjunto na matemática há algumas definições, representações, termos que são semelhantes a qualquer conjunto.
Quando queremos representar ou indicar um conjunto podemos faz isso de algumas formas:
• Pela designação de seus elementos
Para representarmos um conjunto pela designação de seus elementos devemos em primeiro lugar saber quem são os elementos pertencentes a esse conjunto e depois colocar todos esses elementos entre chaves.
Por exemplo: Um conjunto B dos números de dois algarismos que iniciam com a letra D, ficaria assim:
B = {2, 10, 12, 16, 17, 18, 19}
Quando utilizamos essa representação e a quantidade dos elementos do conjunto for muito grande ou infinita podemos colocar reticências entre os elementos ou no final, veja um exemplo:
Um conjunto A dos números de 0 a 101 que começam com a letra C:
A = {5, 50, 51, 52, ... , 100} as reticências estão entre os elementos, isso significa que entre eles existem outros elementos.
Um conjunto H dos números pares.
H = {0, 2, 4, 6, 8, 10, 12, ...} as reticências no final significa que esse conjunto não tem fim.
• Pela propriedade de seus elementos.
Para representarmos um conjunto pela propriedade de seus elementos, basta darmos uma característica que sirva para todos os elementos desse conjunto. Dado um conjunto, para que outro elemento x pertença a esse conjunto ele terá que assumir a mesma característica de todos os outros elementos.
Por exemplo, o conjunto C = {-1, -2, -3, -4, -5, -6,....} está representado pela designação de seus elementos, podendo ser representado da seguinte forma:
C = {x ׀ x é inteiro negativo} está representado pela propriedade de seus elementos.
A leitura dessa representação seria o conjunto C é formado por qualquer valor desde que esse valor seja inteiro negativo.
• Diagramas
Diagrama é outra forma de representarmos um conjunto. Por exemplo, o diagrama do conjunto {0, 1, 2, 3, 4, 5, 6, 7}.
Os elementos que estão dentro da linha fechada são os elementos do conjunto {0, 1, 2, 3, 4, 5, 6, 7}.
Podemos dizer que dois ou mais conjuntos são iguais se os elementos de um forem idênticos aos dos demais, matematicamente representamos uma igualdade pelo sinal =.
Dado o conjunto A = {0, 1, 2, 3, 4} e o conjunto B = {4, 3, 2, 1, 0}, observando os elementos de cada conjunto percebemos que são idênticos, então podemos
dizer que A = B (A igual a B).
Quando comparamos A e B e eles não são iguais dizemos que são diferentes representados assim A ≠ B.
• Relação de inclusão
Ao comparamos dois conjuntos perceberemos que eles nem sempre serão iguais, mas em alguns casos alguns elementos sim. Por exemplo:
Dado o conjunto A = {-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5} e o conjunto B = {0, 1, 2, 3, 4, 5} eles não são diferentes, mas observando o conjunto B veremos que todos os seus elementos estão dentro do conjunto A.
Essa relação é chamada de inclusão, ou seja, o conjunto B está incluso, contido, no conjunto A. Representada matematicamente por B
Dado o conjunto C = {0, 1, 2, 3} e D = {4, 5, 6, 7}, nesses dois conjuntos não é possível aplicar a relação de inclusão, então dizemos que C
• Relação de Pertinência
Essa relação é utilizada quando comparamos conjunto com elementos. Quando queremos dizer que um elemento qualquer está dentro de um conjunto ou que ele não está no conjunto, dizemos que ele pertence ou não pertence a esse determinado conjunto, veja o exemplo:
Dado o conjunto A = {-8, -4, -2, 0, 1, 2, 3}, podemos dizer que - 4 A ( - 4 pertence a A) e que 5 A ( 5 não pertence a A)
www.mundoeducacao.com.br
Comentários
Postar um comentário