Equação reduzida da reta

Marcelo Rigonatto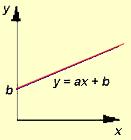

Equação reduzida

Considere ax + by + c = 0 como sendo a equação geral de uma reta não vertical. Isolando y na equação geral obtemos:

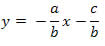
Fazendo

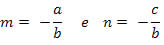
Teremos:

y = mx + q → que é a equação reduzida da reta.

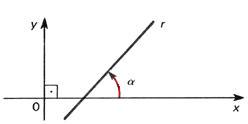
m = tgα, em que α é o ângulo formado entre a reta e o eixo x.
m é chamado de coeficiente angular da reta ou declividade da reta.
q é chamado de coeficiente linear da reta e é o ponto onde a reta corta o eixo x.
Exemplo1. Determine a equação reduzida da reta t que forma um ângulo de 135^o com o eixo das abscissas e que passa pelo ponto P(4, 5).
Solução: Sabemos que α = 135^o e que a equação reduzida da reta é da forma y = mx + q. Assim, temos que:

m = tg 135^o = – 1

Como a reta t passa pelo ponto P, obtemos:

5 = -1*4 + q
q = 5 + 4 = 9
Portanto, a equação reduzida da reta t é y = – x + 9.

Exemplo 2. Determine a equação reduzida da reta s que passa pelos pontos A(1, 0) e B(3, 4).
Solução: Como conhecemos dois pontos da reta s, podemos encontrar sua equação geral.

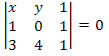
Desenvolvendo o determinante obtemos:

2y – 4x + 4 = 0

Isolando y teremos:

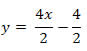
Ou

y = 2x – 2

Observações:
Se a reta for horizontal, ela forma um ângulo nulo com o eixo x. Assim, m = tg 0^o e a equação reduzida da reta será do tipo y = q.
Se a reta for vertical, ela forma um ângulo reto com o eixo x e, como não existe tg 90^o, não é possível escrever a equação reduzida da reta.