Professor de Matemática no Colégio Estadual Dinah Gonçalves
E Biologia na rede privada de Salvador-Bahia
Professor Antonio Carlos carneiro Barroso
email accbarroso@hotmail.com
Blog HTTP://ensinodematemtica.blogspot.com.br e HTTP://accbarroso60.wordpress.com
http://accbarrosogestar.blogspot.com.br
http://accbarrosogestar.blogspot.com.br
Extraído de http://www.alunosonline.com.br
Soma dos Termos de uma PG
Marcos Noé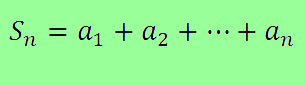
Somando os elementos de uma P.G.
an: posição do termo a ser calculado
a1: primeiro termo
q: razão
n: número de termos
Em algumas situações precisamos determinar a soma dos termos de uma PG, para isso utilizamos a expressão:
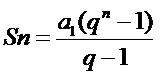
Exemplo 1
Determine a soma dos doze primeiros elementos da progressão geométrica (2, 8, 32, 128, ...).
a1: 2
q (razão): 8 : 2 = 4
n: 12
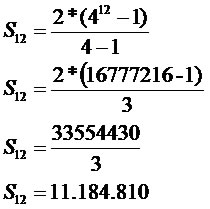
Exemplo 2
Um tipo de bactéria divide-se em duas a cada hora. Após 12 horas, qual será o número de bactérias?
a1: 1
q: 2
n: 12
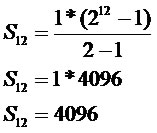
Após 12 horas o número de bactérias será igual a 4096.
Exemplo 3
Ao ser atacada por uma praga desconhecida, os frutos de uma mangueira foram apodrecendo dia após dia, obedecendo a uma progressão geométrica de primeiro termo igual a 2 e razão igual a 3. Se no décimo dia apodreceram os últimos frutos, calcule o número de frutos atacados pela praga.
Resolução:
Podemos analisar a situação da seguinte forma:
Exemplo 3
Ao ser atacada por uma praga desconhecida, os frutos de uma mangueira foram apodrecendo dia após dia, obedecendo a uma progressão geométrica de primeiro termo igual a 2 e razão igual a 3. Se no décimo dia apodreceram os últimos frutos, calcule o número de frutos atacados pela praga.
Resolução:
Podemos analisar a situação da seguinte forma:
1º dia
|
2º dia
|
3º dia
|
4º dia
|
2
|
6
|
18
|
54
|
a1: 2
q: 3
n: 10
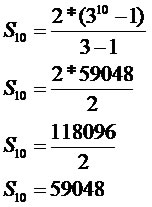
q: 3
n: 10
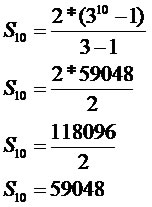
O número de frutos atacados pela praga será de 59.048.
Exemplo 4
Uma pessoa resolve guardar um dinheiro obedecendo a uma progressão geométrica de razão 2. Considerando que no primeiro mês ela irá poupar R$ 0,50, qual será o valor poupado no oitavo mês e o total guardado no período?
Valor guardado no 8º mês.
an = a1*qn–1
a8 = 0,5*28–1
a8 = 0,5*27
a8 = 0,5*128
a8 = 64
No oitavo mês ela irá poupar R$ 64,00.
Total poupado
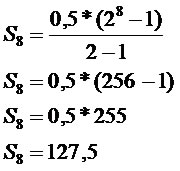
Exemplo 4
Uma pessoa resolve guardar um dinheiro obedecendo a uma progressão geométrica de razão 2. Considerando que no primeiro mês ela irá poupar R$ 0,50, qual será o valor poupado no oitavo mês e o total guardado no período?
Valor guardado no 8º mês.
an = a1*qn–1
a8 = 0,5*28–1
a8 = 0,5*27
a8 = 0,5*128
a8 = 64
No oitavo mês ela irá poupar R$ 64,00.
Total poupado
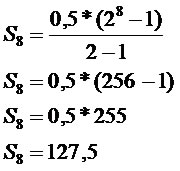
A quantia poupada no tempo determinado é de R$ 127,50.
Nenhum comentário:
Postar um comentário