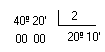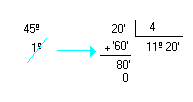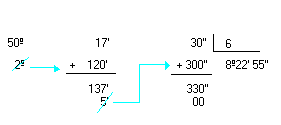Esse é o blog do Professor de Matemática Carlos Barroso. Trabalho no Colégio Estadual Dinah Gonçalves . Valéria-Salvador-Bahia .Inscreva-se Já no meu canal www.youtube.com/accbarroso1 e receba as videoaulas de Matemática.
sábado, 23 de maio de 2020
Adição de números Inteiros
Na soma de dois números inteiros com sinais iguais, o valor absoluto será a soma das parcelas, e o sinal será o mesmo das parcelas.
Exemplo: (+ 5) + (+ 4) = + 9
(- 5) + (- 4) = - 9
Na soma de dois números inteiros com sinais diferentes, o valor absoluto será a diferença das parcelas e o sinal será o da parcela de maior valor absoluto.
Exemplo: (- 5) + (+ 4) = - 1
A Soma de dois números inteiros opostos é ZERO.
Exemplo: (+ 10) + (- 10) = 0
Simplificando a escrita:
a onblur="try {parent.deselectBloggerImageGracefully();} catch(e) {}" href="https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjh-6fJsAdHFmvgzUostGtucG7L2Nfh1PrIHTjCVxBDGzqlugcHsflS1G0QYQmHrarGU41jvAPfLLkYVPwz7w9dU4lN4yNwZzfISyl9XU3P4qIO2-mM_r_ZjCImCwXgg0dG6GUAU_oB-Ew/s1600/soma.JPG">

Propriedades da Adição:
►Propriedade do fechamento
(+15) + (+8) = +23
(-34) + (+20) = -14
(-60) + (+60) = 0
A soma de dois números inteiros é sempre um número inteiro.
► Propriedade Comutativa
(+20) + (-43) = -23
(-43) + (+20) = -23
(+20) + (-43) = (-43) + (+20)
A ordem das parcelas não altera a soma
► Propriedade Associativa
[(+10) + (-6)] + (-80) (+10) + [(-6) + (-80)] =
= (+4) + (-80) = -76 (+10) + (-86) = -76
Numa adição de três ou mais parcelas, podemos associar as parcelas de formas diferentes, que os resultados serão iguais.
►Elemento Neutro
(-32) + 0 = 0 + (-32) = -32
(+250) + 0 = 0 + (+250) = +250
A subtração é uma operação básica da Matemática, sendo representada pelo sinal de –. O desenvolvimento da subtração entre números Naturais é de certa forma bem simples. Observe os exemplos:
10 – 2 = 8
12 – 6 = 6
22 – 10 = 12
52 – 12 = 40
101 – 10 = 91
200 – 189 = 11
As operações de subtração envolvendo os números Inteiros requerem algumas situações teóricas que relacionam os possíveis sinais operatórios. Para realizar a subtração entre os números inteiros precisamos ter conhecimento sobre o módulo de um número. Módulo de um número inteiro é calculado obtendo o seu valor real. Observe:
Módulo de +1: representado por |+1| = 1
| – 3| = 3
| – 7| = 7
Regras operatórias:
Sinais iguais: soma e conserva o sinal.
Sinais diferentes: subtrai e conserva o sinal do maior módulo.
Operações sem parênteses
+ 10 – 7 = + 3 (Sinais diferentes: subtrai e conserva o sinal do maior módulo)
– 3 – 3 = – 6 (Sinais iguais: soma e conserva o sinal)
+ 20 – 30 = – 10 (Sinais diferentes: subtrai e conserva o sinal do maior módulo)
– 12 + 3 = – 9 (Sinais diferentes: subtrai e conserva o sinal do maior módulo)
– 9 + 9 = 0 (operação entre números opostos, resultado sempre será 0)
– 25 + 24 = – 1 (Sinais diferentes: subtrai e conserva o sinal do maior módulo)
Operações com parênteses
Nesse caso, as operações de subtração podem ser resolvidas eliminando os parênteses, isso será feito aplicando algumas regras que envolvem jogo de sinal, observe:
+ (+) = +
+ (–) = –
– (+) = –
– (–) = +
Eliminado os parênteses, passa a valer as regras operatórias:
(+10) – (–23) = +10 + 23 = + 33
(+20) – (+12) = +20 – 12 = + 8
(–32) + (–5) = – 32 – 5 = – 37
(–27) – (–30) = –27 + 30 = + 3
O zero é o elemento neutro da adição.
/www.mundoeducacao.com.br
Exemplo: (+ 5) + (+ 4) = + 9
(- 5) + (- 4) = - 9
Na soma de dois números inteiros com sinais diferentes, o valor absoluto será a diferença das parcelas e o sinal será o da parcela de maior valor absoluto.
Exemplo: (- 5) + (+ 4) = - 1
A Soma de dois números inteiros opostos é ZERO.
Exemplo: (+ 10) + (- 10) = 0
Simplificando a escrita:
a onblur="try {parent.deselectBloggerImageGracefully();} catch(e) {}" href="https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjh-6fJsAdHFmvgzUostGtucG7L2Nfh1PrIHTjCVxBDGzqlugcHsflS1G0QYQmHrarGU41jvAPfLLkYVPwz7w9dU4lN4yNwZzfISyl9XU3P4qIO2-mM_r_ZjCImCwXgg0dG6GUAU_oB-Ew/s1600/soma.JPG">


Propriedades da Adição:
►Propriedade do fechamento
(+15) + (+8) = +23
(-34) + (+20) = -14
(-60) + (+60) = 0
A soma de dois números inteiros é sempre um número inteiro.
► Propriedade Comutativa
(+20) + (-43) = -23
(-43) + (+20) = -23
(+20) + (-43) = (-43) + (+20)
A ordem das parcelas não altera a soma
► Propriedade Associativa
[(+10) + (-6)] + (-80) (+10) + [(-6) + (-80)] =
= (+4) + (-80) = -76 (+10) + (-86) = -76
Numa adição de três ou mais parcelas, podemos associar as parcelas de formas diferentes, que os resultados serão iguais.
►Elemento Neutro
(-32) + 0 = 0 + (-32) = -32
(+250) + 0 = 0 + (+250) = +250
A subtração é uma operação básica da Matemática, sendo representada pelo sinal de –. O desenvolvimento da subtração entre números Naturais é de certa forma bem simples. Observe os exemplos:
10 – 2 = 8
12 – 6 = 6
22 – 10 = 12
52 – 12 = 40
101 – 10 = 91
200 – 189 = 11
As operações de subtração envolvendo os números Inteiros requerem algumas situações teóricas que relacionam os possíveis sinais operatórios. Para realizar a subtração entre os números inteiros precisamos ter conhecimento sobre o módulo de um número. Módulo de um número inteiro é calculado obtendo o seu valor real. Observe:
Módulo de +1: representado por |+1| = 1
| – 3| = 3
| – 7| = 7
Regras operatórias:
Sinais iguais: soma e conserva o sinal.
Sinais diferentes: subtrai e conserva o sinal do maior módulo.
Operações sem parênteses
+ 10 – 7 = + 3 (Sinais diferentes: subtrai e conserva o sinal do maior módulo)
– 3 – 3 = – 6 (Sinais iguais: soma e conserva o sinal)
+ 20 – 30 = – 10 (Sinais diferentes: subtrai e conserva o sinal do maior módulo)
– 12 + 3 = – 9 (Sinais diferentes: subtrai e conserva o sinal do maior módulo)
– 9 + 9 = 0 (operação entre números opostos, resultado sempre será 0)
– 25 + 24 = – 1 (Sinais diferentes: subtrai e conserva o sinal do maior módulo)
Operações com parênteses
Nesse caso, as operações de subtração podem ser resolvidas eliminando os parênteses, isso será feito aplicando algumas regras que envolvem jogo de sinal, observe:
+ (+) = +
+ (–) = –
– (+) = –
– (–) = +
Eliminado os parênteses, passa a valer as regras operatórias:
(+10) – (–23) = +10 + 23 = + 33
(+20) – (+12) = +20 – 12 = + 8
(–32) + (–5) = – 32 – 5 = – 37
(–27) – (–30) = –27 + 30 = + 3
O zero é o elemento neutro da adição.
/www.mundoeducacao.com.br
Poluição das águas Esgoto, petróleo e metais pesados ameaçam águas

Colégio Estadual Dinah Gonçalves
email
accbarroso@hotmail.com
Lixo recolhido em uma praia do litoral baiano
Segundo convenções internacionais, a poluição dos oceanos é a introdução, pelo homem, de substâncias que provoquem, direta ou indiretamente, danos à vida marinha, ameacem a saúde humana ou comprometam a atividade pesqueira. Os principais poluentes do meio marinho são o esgoto doméstico, petróleo e seus derivados, metais pesados, substâncias organocloradas e o lixo.
O termo poluição é utilizado para designar a introdução de qualquer substância que normalmente não existe no ecossistema e à qual os organismos não estão adaptados. Essas substâncias, chamadas de poluentes, provocam a degradação física e química do ambiente.
Esgoto doméstico
O despejo de esgoto não tratado no mar provoca o aumento da matéria orgânica presente na água, levando a uma elevação na quantidade de nutrientes disponíveis. Esse processo é conhecido como eutrofização. O aumento na concentração de nutrientes permite o crescimento rápido e intenso de microalgas marinhas. Após certo tempo, essas algas morrem e são degradadas por bactérias decompositoras.
O processo de decomposição das algas consome o oxigênio dissolvido na água, reduzindo sua disponibilidade para os organismos marinhos. Além disso, a grande quantidade de algas torna a água do mar turva, prejudicando a fotossíntese e reduzindo ainda mais o teor de oxigênio na água.
Outro problema gerado pelo despejo de esgoto é a possibilidade de contaminação da água do mar por microrganismos patogênicos, muitas vezes presentes nas fezes humanas, que podem causar doenças como a hepatite e a cólera. A fim de evitar esses problemas, medidas de saneamento básico, como a fiscalização dos emissores e o tratamento do esgoto doméstico, devem ser adotadas.
Derramamentos de petróleo
O petróleo pode ser liberado no mar de diversas formas: devido a acidentes durante o percurso dos navios transportadores, durante a lavagem dos tanques dos navios, devido a acidentes nos dutos que o conduzem às usinas de refinamento ou por causa de vazamentos nas estações de extração.
Após um derramamento de petróleo, as primeiras horas são as mais críticas, pois é o período de ação da fração volátil do petróleo, que é composta por substâncias extremamente tóxicas. As substâncias voláteis formam uma espécie de bolha letal na atmosfera, que intoxica e mata todos os organismos que respirarem esse ar contaminado.
Musse tóxica
Por outro lado, a fração solúvel do petróleo se alastra pelo mar, atingindo as praias e costões rochosos e também descendo pela coluna d'água. A ação das ondas transforma o petróleo numa espécie de espuma tóxica, chamada de "ponto de musse", que se espalha ainda mais facilmente pelo ambiente.
A fração solúvel do petróleo causa sérios danos à biota marinha. Intoxica e mata os microrganismos presentes no plâncton, gruda nos organismos marinhos, dificultando ou até mesmo impedindo suas funções vitais, recobre os habitantes dos costões rochosos, como os crustáceos e os moluscos, impedindo que eles se alimentem e realizem suas trocas gasosas.
As aves marinhas também podem ser afetadas, pois o petróleo pode grudar em suas penas, impedindo-as de impermeabilizá-las e, às vezes, até mesmo de voar.
Existem algumas bactérias capazes de degradar o petróleo. A eficiência do uso de tais microrganismos para a limpeza de áreas atingidas por derramamentos vem sendo estudada. No entanto, é muito melhor tomar atitudes que evitem ou minimizem as ocorrências de acidentes durante o transporte e a produção do petróleo, evitando ao máximo que esses desastres ecológicos ocorram.
Metais pesados
Certos processos industriais, entre as quais a produção de celulose e de tecidos e a fabricação de tintas e solventes, geram metais pesados, tais como o mercúrio, o chumbo e o cádmio, como resíduos. Caso a indústria não realize o tratamento adequado de seu esgoto, esses metais serão lançados em rios, que acabam por desaguar no mar, contaminando-o.
Os metais pesados se acumulam no organismo e podem causar sérios problemas, como disfunções do sistema nervoso e aumento na incidência de câncer, em animais marinhos e também no homem. Assim, o esgoto industrial deve ser tratado antes de ser despejado em rios. Além disso, os emissários industriais devem ser fiscalizados e monitorados para detectar possíveis descargas de metais pesados.
Contaminação por organoclorados
Os organoclorados, também conhecidos como "poluentes orgânicos persistentes", ou simplesmente POPs, pois não se degradam facilmente na natureza, são substâncias que se originam, principalmente, na produção de pesticidas e plásticos.
Os POPs não são solúveis em água. No entanto, são extremamente solúveis em lipídios. Por isso, se acumulam na gordura dos animais, afetando toda a cadeia alimentar. Essas substâncias podem causar sérios danos aos organismos, afetando seu sistema nervoso, circulatório, imunológico e reprodutor.
Um exemplo de organoclorado é o pesticida chamado de DDT. Nos anos 70, quando seus efeitos nocivos ainda não eram conhecidos, ele foi amplamente utilizado no combate a pragas agrícolas, chegando aos oceanos através da água das chuvas, carregado pelo ar e pelo acúmulo na cadeia alimentar. Atualmente seu uso é proibido, porém, devido ao seu acúmulo nos organismos, ainda podemos encontrá-lo nos oceanos e nos organismos marinhos.
Lixo
Todos os anos, centenas de toneladas de lixo chegam às praias de todo o mundo trazidas pelo mar. Uma das principais fontes do lixo nos oceanos são as embarcações, tais como veleiros, cargueiros ou navios turísticos, que despejam seu lixo diretamente no mar. Outra fonte de dejetos é a descarga em rios próximos à zona costeira ou diretamente nas praias; a ação das correntes e das ondas acaba por espalhar esse lixo pelo oceano.
O lixo jogado no mar representa uma séria ameaça aos organismos marinhos. Muitos animais, como as tartarugas marinhas e os golfinhos, confundem pedaços de plástico ou vidro com os seus alimentos, engolindo-os e morrendo sufocados. No Brasil, existe o registro do caso de um filhote de baleia jubarte que morreu de inanição, após ingerir tampinhas de garrafas plásticas que ficaram presas em sua garganta, impedindo a passagem do leite materno.
Medidas de proteção aos oceanos
Para evitar as agressões ao meio marinho, convenções internacionais determinam que todas as embarcações devem manter os resíduos produzidos a bordo em recipientes, sendo proibido e passível de multa o seu descarte no mar. No entanto, uma vez que não se pode identificar precisamente a origem dos dejetos, a fiscalização dessas ações é extremamente difícil.
Como pudemos ver, existem diversas e perigosas fontes de poluição que ameaçam o ambiente marinho. Para continuarmos a usufruir da enorme fonte de biodiversidade e recursos naturais que o mar representa, precisamos repensar nossas atitudes. Assim, além de desenvolver técnicas de recuperação de áreas degradadas, é fundamental a adoção de medidas de proteção que evitem novas contaminações e danos ao ecossistema marinho.
Alice Dantas Brites
Análise Combinatória
O estudo da análise combinatória nos permite descobrir quais são as diferentes possibilidades de uma combinação de variáveis. Por exemplo, quantas placas de carro são possíveis de existir no sistema atual de placas brasileiro. É uma matéria bastante cobrada em vestibulares e concursos públicos, pois envolve um pensamento mais abstrato, pois na maioria das vezes, não enxergamos todas as possibilidades.
A explicação dessa matéria é muito mais fácil quando utilizamos exemplos. Então, supondo que um restaurante “À la carte” tenha disponível 2 tipos de bifes, 2 tipos de arroz, 2 tipos de feijão e 3 tipos de bebidas. O dono do restaurante queira servir pratos contendo 1 elemento de cada tipo de comida. Nomeando os tipos de comida da forma “bife 1, arroz 1, arroz 2 … bebida 1, bebida 2, etc”, montamos o esquema:

[analise combinatoria - esquema]
Se formos seguir os caminhos descritos pelas linhas, encontraremos 24 caminhos, que são o total de possibilidades de pratos diferentes. Perceba que quanto mais opções de comidas, maior e mais complexo fica o esquema. Então, imagine como seria descobrir as possibilidades das placas de carro no sistema brasileiro? (três letras, 4 algarismos).
Mas podemos calcular de forma diferente. Basta multiplicar todas as opções de comida disponiveis: 2 . 2 . 2 . 3 = 24
www.infoescola.com
A explicação dessa matéria é muito mais fácil quando utilizamos exemplos. Então, supondo que um restaurante “À la carte” tenha disponível 2 tipos de bifes, 2 tipos de arroz, 2 tipos de feijão e 3 tipos de bebidas. O dono do restaurante queira servir pratos contendo 1 elemento de cada tipo de comida. Nomeando os tipos de comida da forma “bife 1, arroz 1, arroz 2 … bebida 1, bebida 2, etc”, montamos o esquema:

[analise combinatoria - esquema]
Se formos seguir os caminhos descritos pelas linhas, encontraremos 24 caminhos, que são o total de possibilidades de pratos diferentes. Perceba que quanto mais opções de comidas, maior e mais complexo fica o esquema. Então, imagine como seria descobrir as possibilidades das placas de carro no sistema brasileiro? (três letras, 4 algarismos).
Mas podemos calcular de forma diferente. Basta multiplicar todas as opções de comida disponiveis: 2 . 2 . 2 . 3 = 24
www.infoescola.com
Probabilidade e Genética
Os cálculos envolvendo probabilidades estão presentes nas situações ligadas à genética, abrangendo diversos estudos relacionados às leis de Mendel. Vamos utilizar as noções de probabilidade na determinação do sexo dos filhos de um casal. Suponhamos que um casal deseja ter dois filhos e quer saber qual a probabilidade de ocorrer os seguintes pares:
Dois meninos;
Duas meninas;
Um menino e uma menina.
Para determinarmos a probabilidade do sexo dos filhos, precisamos saber as seguintes condições:
O sexo do segundo filho independe do sexo do primeiro, e assim sucessivamente.
As chances de ter um menino são iguais às chances de ter uma menina, isto é, 50%. Portanto, temos:
Menino = 1/2 = 50%
Menina = 1/2 = 50%
Com base nesses dados, vamos determinar as chances de ocorrer os pares fornecidos anteriormente. Para tal situação, utilizamos um desenvolvimento binomial dado por
(x + y)n, onde n equivale ao número de filhos que o casal deseja ter. Nesse binômio, x representará menino e y, menina. Observe o desenvolvimento da expressão:
(x + y)2 → (x + y) * (x + y) → x² + xy + xy + y² → x² + 2xy + y²
x (menino) = 1/2
y (menina) = 1/2
Dois meninos → x² → (1/2)² → 1/4 → 25%
Duas meninas → y² → (1/2)² → 1/4 → 25%
Um menino e uma menina → 2xy → 2 * 1/2 * 1/2 → 2/4 → 1/2 → 50%
Supondo que um casal deseja ter três filhos, determine as possibilidades e probabilidades dos filhos desejados pelo casal.
(x + y)3 → (x + y) * (x + y) * (x + y) → x³ + 3x²y + 3xy² + y³
Três meninos → x³ → (1/2)³ → 1/8 → 12,5%
Dois meninos e uma menina → 3x²y → 3 * (1/2)² * 1/2 → 3 * 1/4 * 1/2 → 3/8 → 37,5%
Duas meninas e um menino → 3xy² → 3 * 1/2 * (1/2)² → 3 * 1/2 * 1/4 → 3/8 → 37,5%
Três meninas → y³ → (1/2)³ → 1/8 → 12,5%
Dois meninos;
Duas meninas;
Um menino e uma menina.
Para determinarmos a probabilidade do sexo dos filhos, precisamos saber as seguintes condições:
O sexo do segundo filho independe do sexo do primeiro, e assim sucessivamente.
As chances de ter um menino são iguais às chances de ter uma menina, isto é, 50%. Portanto, temos:
Menino = 1/2 = 50%
Menina = 1/2 = 50%
Com base nesses dados, vamos determinar as chances de ocorrer os pares fornecidos anteriormente. Para tal situação, utilizamos um desenvolvimento binomial dado por
(x + y)n, onde n equivale ao número de filhos que o casal deseja ter. Nesse binômio, x representará menino e y, menina. Observe o desenvolvimento da expressão:
(x + y)2 → (x + y) * (x + y) → x² + xy + xy + y² → x² + 2xy + y²
x (menino) = 1/2
y (menina) = 1/2
Dois meninos → x² → (1/2)² → 1/4 → 25%
Duas meninas → y² → (1/2)² → 1/4 → 25%
Um menino e uma menina → 2xy → 2 * 1/2 * 1/2 → 2/4 → 1/2 → 50%
Supondo que um casal deseja ter três filhos, determine as possibilidades e probabilidades dos filhos desejados pelo casal.
(x + y)3 → (x + y) * (x + y) * (x + y) → x³ + 3x²y + 3xy² + y³
Três meninos → x³ → (1/2)³ → 1/8 → 12,5%
Dois meninos e uma menina → 3x²y → 3 * (1/2)² * 1/2 → 3 * 1/4 * 1/2 → 3/8 → 37,5%
Duas meninas e um menino → 3xy² → 3 * 1/2 * (1/2)² → 3 * 1/2 * 1/4 → 3/8 → 37,5%
Três meninas → y³ → (1/2)³ → 1/8 → 12,5%
Função Composta
A função composta pode ser entendida pela determinação de uma terceira função C, formada pela junção das funções A e B. Matematicamente falando, temos que f: A → B e g: B → C, denomina a formação da função composta de g com f, h: A → C. Dizemos função g composta com a função f, representada por gof.
Exemplo 1
Ao considerarmos as funções f(x) = 4x e g(x) = x² + 5, determinaremos:
a) g o f
(g o f)(x) = g(f(x))
g(x) = x² + 5
g(4x) = (4x)² + 5
g(4x) = 16x² + 5
(g o f)(x) = g(f(x)) = 16x² + 5
b) f o g
(f o g)(x) = f(g(x))
f(x) = 4x
f(x² + 5) = 4 * (x² + 5)
f(x² + 5) = 4x² + 20
(f o g)(x) = f(g(x)) = 4x² + 20
Exemplo 2
Vamos determinar g(f(x)) e f(g(x)), em relação às funções f(x) = x + 2 e g(x) = 4x² – 1.
(g o f)(x) = g(f(x))
g(x) = 4x² – 1
g(x + 2) = 4 * (x + 2)² – 1
g(x + 2) = 4 * (x + 2) * (x + 2) – 1
g(x + 2) = 4 * (x² + 2x + 2x + 4) – 1
g(x + 2) = 4 * (x² + 4x + 4) – 1
g(x + 2) = 4x² + 16x + 16 – 1
g(x + 2) = 4x² + 16x + 15
(g o f)(x) = g(f(x)) = 4x² + 16x + 15
(f o g)(x) = f(g(x))
f(x) = x + 2
f(4x² – 1) = (4x² – 1) + 2
f(4x² – 1) = 4x² – 1 + 2
f(4x² – 1) = 4x² + 1
(f o g)(x) = f(g(x)) = 4x² + 1
Marcos Noé
Exemplo 1
Ao considerarmos as funções f(x) = 4x e g(x) = x² + 5, determinaremos:
a) g o f
(g o f)(x) = g(f(x))
g(x) = x² + 5
g(4x) = (4x)² + 5
g(4x) = 16x² + 5
(g o f)(x) = g(f(x)) = 16x² + 5
b) f o g
(f o g)(x) = f(g(x))
f(x) = 4x
f(x² + 5) = 4 * (x² + 5)
f(x² + 5) = 4x² + 20
(f o g)(x) = f(g(x)) = 4x² + 20
Exemplo 2
Vamos determinar g(f(x)) e f(g(x)), em relação às funções f(x) = x + 2 e g(x) = 4x² – 1.
(g o f)(x) = g(f(x))
g(x) = 4x² – 1
g(x + 2) = 4 * (x + 2)² – 1
g(x + 2) = 4 * (x + 2) * (x + 2) – 1
g(x + 2) = 4 * (x² + 2x + 2x + 4) – 1
g(x + 2) = 4 * (x² + 4x + 4) – 1
g(x + 2) = 4x² + 16x + 16 – 1
g(x + 2) = 4x² + 16x + 15
(g o f)(x) = g(f(x)) = 4x² + 16x + 15
(f o g)(x) = f(g(x))
f(x) = x + 2
f(4x² – 1) = (4x² – 1) + 2
f(4x² – 1) = 4x² – 1 + 2
f(4x² – 1) = 4x² + 1
(f o g)(x) = f(g(x)) = 4x² + 1
Marcos Noé
Procariontes

Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
Escherichia coli, um procarionte.
O Reino Monera compreende os seres procariontes. Entretanto, a expressão citada se encontra cada vez em desuso, uma vez que atualmente compreende-se que os organismos classificados neste reino não possuem grau de parentesco tão próximo quanto se imaginava. Assim, os reinos Archaea e Bactéria compreendem os procariontes antes considerados reino Monera.
Mais recentemente, foi proposta uma classificação na qual os seres vivos são divididos em três domínios: Arquea, Bacteria e Eukarya, nos quais unicamente os dois primeiros possuem esses representantes.
Assim, como são seres unicelulares, descrever a estrutura dos seres do Arquea e Bactéria é a própria descrição da célula procarionte, cuja forma simples é, em geral, esférica ou em bastonete, mas pode também ser em bastonete curto ou hélice, podendo formar colônias.
Assim, procariontes possuem como envoltório cápsula, parede (constituída de peptidioglicanos) e membrana citoplasmática sem esteróis – essa pode formar invaginações ou dobras, chamadas mesossomos. A respiração se dá pela membrana citoplasmática, o cromossomo fibrilar é único, citoesqueleto ausente e núcleo disperso no citoplasma - sua característica mais conhecida, uma vez que não possui uma membrana envolvendo os cromossomos.
Sobre o citoplasma, esse possui apenas DNA circular que não se condensa e tampouco é ligado a proteínas, ribossomos e grãos de glicogênio. Pode haver, ainda: moléculas menores de DNA, chamadas plasmídeos e flagelos, que auxiliam na locomoção. Pêlos também podem ocorrer, auxiliando no ajustamento do indivíduo às células do hospedeiro e na conjugação, uma vez que não se dividem por mitose. Sobre isso podemos dizer que os procariontes se reproduzem assexuadamente por conjugação, divisão binária e transdução.
As células que realizam fotossíntese possuem algumas membranas associadas aos pigmentos responsáveis pela captação de energia luminosa e são denominadas autotróficas, assim como as que usam a energia química para produzir compostos orgânicos. Entretanto, a maioria dos indivíduos procariontes são heterotróficos por absorção, realizando vários tipos de fermentação e vários tipos de respiração.
Alguns procariontes podem causar doenças em humanos. São elas: botulismo, cólera, coqueluche, difteria, febre maculosa, hanseníase, leptospirose, meningite, pneumonia, sífilis, tétano e tuberculose.
Por Mariana Araguaia
Graduada em Biologia
Equações logaritmicas
Os logaritmos possuem várias aplicações na Matemática e em diversas áreas do conhecimento, como Física, Biologia, Química, Medicina, Geografia entre outras. Iremos através de exemplos demonstrar a utilização das técnicas de logaritmos na busca de resultados para as variadas situações em questão.
Exemplo 1 – Matemática Financeira
Uma pessoa aplicou a importância de R$ 500,00 numa instituição bancária que paga juros mensais de 3,5%, no regime de juros compostos. Quanto tempo após a aplicação o montante será de R$ 3 500,00?
Resolução:
Nos casos envolvendo a determinação do tempo e juros compostos, a utilização das técnicas de logaritmos é imprescindível.
Fórmula para o cálculo dos juros compostos: M = C * (1 + i)t. De acordo com a situação problema, temos:
M (montante) = 3500
C (capital) = 500
i (taxa) = 3,5% = 0,035
t = ?
M = C * (1 + i)t
3500 = 500 * (1 + 0,035)t
3500/500 = 1,035t
1,035t = 7
Aplicando logaritmo
log 1,035t = log 7
t * log 1,035 = log 7 (utilize tecla log da calculadora científica )
t * 0,0149 = 0,8451
t = 0,8451 / 0,0149
t = 56,7
O montante de R$ 3 500,00 será originado após 56 meses de aplicação.
Exemplo 2 – Geografia
Em uma determinada cidade, a taxa de crescimento populacional é de 3% ao ano, aproximadamente. Em quantos anos a população desta cidade irá dobrar, se a taxa de crescimento continuar a mesma?
População do ano-base = P0
População após um ano = P0 * (1,03) = P1
População após dois anos = P0 * (1,03)2= P2
População após x anos = P0 * (1,03)x = Px
Vamos supor que a população dobrará em relação ao ano-base após x anos, sendo assim, temos:
Px = 2*P0
P0 * (1,03)x = 2 * P0
1,03x = 2
Aplicando logaritmo
log 1,03x = log 2
x * log 1,03 = log2
x * 0,0128 = 0,3010
x = 0,3010 / 0,0128
x = 23,5
A população dobrará em aproximadamente 23,5 anos.
Exemplo 3 – Química
Determine o tempo que leva para que 1000 g de certa substância radioativa, que se desintegra a taxa de 2% ao ano, se reduza a 200 g. Utilize a seguinte expressão:
Q = Q0 * e–rt, em que Q é a massa da substância, r é a taxa e t é o tempo em anos.
Q = Q0 * e–rt
200 = 1000 * e–0,02t
200/1000 = e–0,02t
1/5 = e–0,02t (aplicando definição)
–0,02t = loge1/5
–0,02t = loge5–1
–0,02t = –loge5
–0,02t = –ln5 x(–1)
0,02t = ln5
t = ln5 / 0,02
t = 1,6094 / 0,02
t = 80,47
A substância levará 80,47 anos para se reduzir a 200 g.
Os logaritmos criados por John Napier e Jobst Burgi, e posteriormente adaptados por Henry Briggs, possuem a seguinte lei de formação:
logab = x, onde:
a = base do logaritmo
b = logaritmando
x = logaritmo
O logaritmo de um número b em uma base a é o expoente x que se deve aplicar à base a para se ter o número b. Dessa forma:
logab = x ↔ ax = b
Exemplos:
log39 ↔ 32 = 9
log10100 ↔ 102 = 100
log216 ↔ 24 = 16
log981 ↔ 92 = 81
A partir dessa definição podemos apresentar algumas definições que auxiliarão no desenvolvimento de algumas situações envolvendo logaritmo. Veja:
O logaritmo do número 1 em qualquer base sempre será igual a 0.
loga1 = 0, pois a0 = 1
O logaritmo de qualquer número a na própria base a será igual a 1.
logaa = 1, pois a1 = a
O logaritmo de uma potência da base é o expoente, em qualquer base.
logaam = m, pois m * logaa = m * 1 = m
A potência de base a e expoente logab é igual a b.
alogab = b, pois logab = x → ax = b
Dois logaritmos são iguais, quando seus logaritmandos forem iguais.
logab = logac ↔ b = c
Exemplos
Aplicar a definição de logaritmo para calcular o valor de x em cada caso:
a) log327 = x → 3x = 27 → x = 3
b) log81x = 3/4 → x = 813/4 → x = (34)3/4 → x = 312/4 → x = 33 → x = 27
c) log4√2 = x → 4x = √2 → 22x = √2 → 22x = 21/2 → 2x = 1/2 → x = 1/4
d) logx8 = 2 → x2 = 8 → √x = √8 → x = 2√2
e) log4(2x – 1) = 1/2 → 2x – 1 = 41/2 → 2x – 1 = √4 → 2x – 1 = 2 → 2x = 3 → x = 3/2
f) log1818 = x → 18x = 18 → x = 1
g) logx1024 = 2 → x2 = 1024 → √x² = √1024 → x = 32
h) log40,25 = x → 4x = 0,25 → 4x = 25/100 → 4x = 1/4 → 4x = 4–1 → x = –1
i) 16log25 = (24)log25 = (2log25)4 = 54 = 625
j) log0,01 = x → 10x = 0,01 → 10x = 1/100 → 10x = 10–2 → x = –2
Os logaritmos foram criados no intuito de facilitar os cálculos envolvendo números muito grandes ou muito pequenos. Os logaritmos reduzem esses números a algumas bases, a mais utilizada é a base decimal. As propriedades operatórias dos logaritmos possuem o objetivo de transformar multiplicações em somas, divisões em subtrações, potenciações em multiplicações e radiciações em divisões. Essas transformações facilitam os cálculos mais extensos.
Logaritmo de um produto
Considerando a, b e c números reais positivos e a ≠ 1, temos a seguinte propriedade:
loga(b*c) = logab + logac
Exemplo 1
Dados log2 = 0,301 e log3 = 0,477, determine o log12.
log12 → log12 = log(2 * 2 * 3) → log12 = log2 + log2 + log3 → log12 = 0,301 + 0,301 + 0,477 → log 12 = 1,079
Exemplo 2
Determine o valor de log2(8*32).
log2(8*32) = log28 + log232 = 3 + 5 = 8
Logaritmo de um quociente
Considerando a, b e c números reais positivos e a ≠ 1, temos a seguinte propriedade:
loga(b/c) = logab – logac
Exemplo 3
Sabendo que log30 = 1,477 e log5 = 0,699, determine log6.
log6 = (30/5) = log30 – log5 = 1,477 – 0,699 = 0,778
Exemplo 4
log3(6561/81) = log36561 – log381 = 8 – 4 = 5
Logaritmo de uma potência
Considerando a e b números reais positivos, com a ≠ 1, e m um número real, temos a seguinte propriedade:
logabm = m * logab
Exemplo 5
Sabendo que log 2 = 0,3010, calcule o valor de log 64.
log 64 = log 26 = 6 * log 2 = 6 * 0,3010 = 1,806
Exemplo 6
Dado log 2x = 2,4 e log 2 = 0,3, calcule x.
log 2x = 2,4 → x*log 2 = 2,4 → x * 0,3 = 2,4 → x = 2,4/0,3 → x = 8
Mudança de base
Para passarmos logab, com a e b positivos e a ≠ 1, para a base c, com c > 0 e c ≠ 1, utilizamos a seguinte expressão:
logab = logcb/ logca, com logca ≠ 0
Exemplo 7
Passando log49 para a base 2.
log49 = log29 / log24 = log29 / 2
Exemplo 8
Sabendo que log 4 = 0,60 e log 5 = 0,70, calcule log54.
log54 = log4 / log5 = 0,60 / 0,70 → log54 = 0,86
www.mundoeducacao.com.br
Exemplo 1 – Matemática Financeira
Uma pessoa aplicou a importância de R$ 500,00 numa instituição bancária que paga juros mensais de 3,5%, no regime de juros compostos. Quanto tempo após a aplicação o montante será de R$ 3 500,00?
Resolução:
Nos casos envolvendo a determinação do tempo e juros compostos, a utilização das técnicas de logaritmos é imprescindível.
Fórmula para o cálculo dos juros compostos: M = C * (1 + i)t. De acordo com a situação problema, temos:
M (montante) = 3500
C (capital) = 500
i (taxa) = 3,5% = 0,035
t = ?
M = C * (1 + i)t
3500 = 500 * (1 + 0,035)t
3500/500 = 1,035t
1,035t = 7
Aplicando logaritmo
log 1,035t = log 7
t * log 1,035 = log 7 (utilize tecla log da calculadora científica )
t * 0,0149 = 0,8451
t = 0,8451 / 0,0149
t = 56,7
O montante de R$ 3 500,00 será originado após 56 meses de aplicação.
Exemplo 2 – Geografia
Em uma determinada cidade, a taxa de crescimento populacional é de 3% ao ano, aproximadamente. Em quantos anos a população desta cidade irá dobrar, se a taxa de crescimento continuar a mesma?
População do ano-base = P0
População após um ano = P0 * (1,03) = P1
População após dois anos = P0 * (1,03)2= P2
População após x anos = P0 * (1,03)x = Px
Vamos supor que a população dobrará em relação ao ano-base após x anos, sendo assim, temos:
Px = 2*P0
P0 * (1,03)x = 2 * P0
1,03x = 2
Aplicando logaritmo
log 1,03x = log 2
x * log 1,03 = log2
x * 0,0128 = 0,3010
x = 0,3010 / 0,0128
x = 23,5
A população dobrará em aproximadamente 23,5 anos.
Exemplo 3 – Química
Determine o tempo que leva para que 1000 g de certa substância radioativa, que se desintegra a taxa de 2% ao ano, se reduza a 200 g. Utilize a seguinte expressão:
Q = Q0 * e–rt, em que Q é a massa da substância, r é a taxa e t é o tempo em anos.
Q = Q0 * e–rt
200 = 1000 * e–0,02t
200/1000 = e–0,02t
1/5 = e–0,02t (aplicando definição)
–0,02t = loge1/5
–0,02t = loge5–1
–0,02t = –loge5
–0,02t = –ln5 x(–1)
0,02t = ln5
t = ln5 / 0,02
t = 1,6094 / 0,02
t = 80,47
A substância levará 80,47 anos para se reduzir a 200 g.
Os logaritmos criados por John Napier e Jobst Burgi, e posteriormente adaptados por Henry Briggs, possuem a seguinte lei de formação:
logab = x, onde:
a = base do logaritmo
b = logaritmando
x = logaritmo
O logaritmo de um número b em uma base a é o expoente x que se deve aplicar à base a para se ter o número b. Dessa forma:
logab = x ↔ ax = b
Exemplos:
log39 ↔ 32 = 9
log10100 ↔ 102 = 100
log216 ↔ 24 = 16
log981 ↔ 92 = 81
A partir dessa definição podemos apresentar algumas definições que auxiliarão no desenvolvimento de algumas situações envolvendo logaritmo. Veja:
O logaritmo do número 1 em qualquer base sempre será igual a 0.
loga1 = 0, pois a0 = 1
O logaritmo de qualquer número a na própria base a será igual a 1.
logaa = 1, pois a1 = a
O logaritmo de uma potência da base é o expoente, em qualquer base.
logaam = m, pois m * logaa = m * 1 = m
A potência de base a e expoente logab é igual a b.
alogab = b, pois logab = x → ax = b
Dois logaritmos são iguais, quando seus logaritmandos forem iguais.
logab = logac ↔ b = c
Exemplos
Aplicar a definição de logaritmo para calcular o valor de x em cada caso:
a) log327 = x → 3x = 27 → x = 3
b) log81x = 3/4 → x = 813/4 → x = (34)3/4 → x = 312/4 → x = 33 → x = 27
c) log4√2 = x → 4x = √2 → 22x = √2 → 22x = 21/2 → 2x = 1/2 → x = 1/4
d) logx8 = 2 → x2 = 8 → √x = √8 → x = 2√2
e) log4(2x – 1) = 1/2 → 2x – 1 = 41/2 → 2x – 1 = √4 → 2x – 1 = 2 → 2x = 3 → x = 3/2
f) log1818 = x → 18x = 18 → x = 1
g) logx1024 = 2 → x2 = 1024 → √x² = √1024 → x = 32
h) log40,25 = x → 4x = 0,25 → 4x = 25/100 → 4x = 1/4 → 4x = 4–1 → x = –1
i) 16log25 = (24)log25 = (2log25)4 = 54 = 625
j) log0,01 = x → 10x = 0,01 → 10x = 1/100 → 10x = 10–2 → x = –2
Os logaritmos foram criados no intuito de facilitar os cálculos envolvendo números muito grandes ou muito pequenos. Os logaritmos reduzem esses números a algumas bases, a mais utilizada é a base decimal. As propriedades operatórias dos logaritmos possuem o objetivo de transformar multiplicações em somas, divisões em subtrações, potenciações em multiplicações e radiciações em divisões. Essas transformações facilitam os cálculos mais extensos.
Logaritmo de um produto
Considerando a, b e c números reais positivos e a ≠ 1, temos a seguinte propriedade:
loga(b*c) = logab + logac
Exemplo 1
Dados log2 = 0,301 e log3 = 0,477, determine o log12.
log12 → log12 = log(2 * 2 * 3) → log12 = log2 + log2 + log3 → log12 = 0,301 + 0,301 + 0,477 → log 12 = 1,079
Exemplo 2
Determine o valor de log2(8*32).
log2(8*32) = log28 + log232 = 3 + 5 = 8
Logaritmo de um quociente
Considerando a, b e c números reais positivos e a ≠ 1, temos a seguinte propriedade:
loga(b/c) = logab – logac
Exemplo 3
Sabendo que log30 = 1,477 e log5 = 0,699, determine log6.
log6 = (30/5) = log30 – log5 = 1,477 – 0,699 = 0,778
Exemplo 4
log3(6561/81) = log36561 – log381 = 8 – 4 = 5
Logaritmo de uma potência
Considerando a e b números reais positivos, com a ≠ 1, e m um número real, temos a seguinte propriedade:
logabm = m * logab
Exemplo 5
Sabendo que log 2 = 0,3010, calcule o valor de log 64.
log 64 = log 26 = 6 * log 2 = 6 * 0,3010 = 1,806
Exemplo 6
Dado log 2x = 2,4 e log 2 = 0,3, calcule x.
log 2x = 2,4 → x*log 2 = 2,4 → x * 0,3 = 2,4 → x = 2,4/0,3 → x = 8
Mudança de base
Para passarmos logab, com a e b positivos e a ≠ 1, para a base c, com c > 0 e c ≠ 1, utilizamos a seguinte expressão:
logab = logcb/ logca, com logca ≠ 0
Exemplo 7
Passando log49 para a base 2.
log49 = log29 / log24 = log29 / 2
Exemplo 8
Sabendo que log 4 = 0,60 e log 5 = 0,70, calcule log54.
log54 = log4 / log5 = 0,60 / 0,70 → log54 = 0,86
www.mundoeducacao.com.br
Poríferos (porifera)

Animais dotados de poros por todo o corpo, por isso chamados de poríferos, e com um aspecto esponjoso, macio e flexível, podendo ser usados como esponja de banho. São também chamados de espongiários. Predominantemente aquáticos e marinhos, existindo uma família de água doce, a Spongillidae.
Sempre vivem fixos a um substrato, podem estar isolados ou em colônias; são diblásticos, filtradores, possuem um esqueleto silicoso ou calcáreo, não possuem sistema muscular, nervoso e sem diferenciação entre órgãos, por isso chamados parazoários.
Digestão
As esponjas não possuem sistema digestório, e a digestão é exclusivamente intracelular. Se alimentam de pequenas partículas em suspensão na água que circula em seu corpo. Estas partículas entram pelos poros junto com a água, caindo no átrio (ou espongiocele) que é a cavidade interna da esponja e saem pelo ósculo, uma abertura maior. As partículas de alimento que ali entram podem ficar retidas no colarinho de células flageladas chamadas coanócitos, que promovem a movimentação e circulação de água no átrio da esponja, graças à presença de flagelos.
Os coanócitos fagocitam e digerem parcialmente estas partículas, transferindo-as para os amebócitos, células que compoem a mesogléia, material gelatinoso que preenche o corpo das esponjas. Os amebócitos terminam de digerir as partículas e distribuir por todo o corpo o produto desta digestão.


Sistema nervoso
As esponjas não apresentam sistema nervoso.
Respiração
Também não apresentam sistema respiratório, e as trocas gasosas ocorrem por difusão.
Circulação
A circulação é basicamente de água, alimento e espermatozóides, que entram pelos poros e saem pelo ósculo, promovida pelo movimento dos flagelos dos coanócitos
Excreção
A excreção é feita por difusão.
Tegumento e esqueleto
Espículas
A parte externa do corpo das esponjas apresenta muitos poros e é formada por células achatadas denominadas pinacócitos, formando a pinacoderme. Os coanócitos também participam desse revestimento.
Na mesogléia existem espículas, estruturas de sustentação que podem ser de calcário ou sílica. As espículas se assemelham com agulhas. Pode possuir também uma rede de proteína, chamada espongina.
Reprodução
Os poríferos podem se reproduzir das seguintes formas:

Assexuada
- Brotamento: surge um broto no corpo da esponja, que pode se soltar e dar origem à um novo indivíduo.
- Fragmentação: pequenos fragmentos de uma esponja podem dar origem a novos indivíduos, pois as esponjas possuem um grande poder de regeneração.
Gêmula
- Gemulação: ocorre em espécies de água doce. Formam-se gêmulas, estruturas de resistência que se formam no interior do corpo da esponja. São compostas por células indiferenciadas e protegidas por um envoltório rígido.
Sexuada: a maior parte das esponjas é hermafrodita. Os gametas são formados em células chamadas gonócitos, que são derivadas dos amebócitos. Os espermatozóides saem da esponja pelo ósculo e penetram em outra esponja pelos poros, junto com a corrente de água. São captados pelos coanócitos e transferidos até os óvulos, que ficam na mesogléia, e promovem a fecundação. Do ovo surgirá uma larva ciliada, de vida livre, que abandona a esponja e nada até se fixar em um substrato e dar origem a um novo indivíduo.

Por Fabiana Santos Gonçalves
Polinômios - Exercícios resolvidos
Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
Polinômios - Exercícios resolvidos
01. Calcular o valor numérico do polinômio P(x) = x3 - 7x2 + 3x - 4 para x = 2.
RESOLUÇÃO: P(2) = -18
02. Determinar os valores reais de a e b para que o polinômio x3 + 6x2 + ax + b seja um cubo perfeito.
RESOLUÇÃO: a = 12 e b = 8
03. (UESB) Se P(x) = xn - xn-1 + xn-2 - ... + x2 - x + 1 e P(-1) = 19, então n é igual a:
a) 10
b) 12s
c) 14
d) 16
e) 18
RESPOSTA: E
04. (UBERL) Se P(x) é um polinômio tal que 2P(x) + x2 P(x - 1) ≡ x3 + 2x + 2, então P(1) é igual a:
a) 0
b) -1
c) 1
d) -2
e) 2
RESPOSTA: E
05. As soluções da equação Q(x) = 0, em que Q(x) é o quociente do polinômio x4 - 10x3 + 24x2 + 10x - 24 por x2 - 6x + 5, são:
a) -1 e 5
b) -1 e -5
c) 1 e -5
d) 1 e 5
e) 0 e 1
RESPOSTA: A
06. (UESP) Se o polinômio P(x) = x3 + mx2 - 1 é divisível por x2 + x - 1, então m é igual a:
a) -3
b) -2
c) -1
d) 1
e) 2
RESPOSTA: E
07. (UEL) Dividindo-se o polinômio x4 + 2x3 - 2x2 - 4x - 21 por x + 3, obtêm-se:
a) x3 - 2x2 + x -12 com resto nulo;
b) x3 - 2x2 + 3 com resto 16;
c) x3 - x2 -13x + 35 e resto 84;
d) x3 - x2 - 3x + 1com resto 2;
e) x3 - x2 + x -7 e resto nulo;
RESPOSTA: E
08. (UEL) Se o resto da divisão do polinômio p = x4 - 4x3 - kx - 75 por (x - 5) é 10, o valor de k é:
a) -5
b) -4
c) 5
d) 6
e)
RESPOSTA: E
09. Sejam m e n determinados de tal modo que o polinômio x4 - 12x3 + 47x2 + mx + n seja divisível por x2 - 7x + 6. Então m + n é igual a:
a) 72
b) 0
c) -36
d) 36
e) 58
RESPOSTA: C
10. Para que o polinômio 2x4 - x3 + mx2 - nx + 2 seja divisível por x2 - x - 2, devemos ter:
a) m = 1 e n = 6
b) m = -6 e n = -1
c) m = 6 e n = 1
d) m = -6 e n = 1
e) m = 6 e n = -1
RESPOSTA: D
www.colaweb.com
Artrópodes

Dois artrópodes da classe insecta. Fotografia: Fabrício Oda.
Dentro do estudo dos invertebrados, o filo Arthropoda merece atenção especial por possuir o maior número de espécies do reino animal, agrupando mais de 800 mil exemplares, habitantes das mais diversas regiões do globo terrestre.
São triblásticos, protostômios e celomados. O corpo articulado, organizado em cabeça, tórax e abdome ou cefalotórax e abdômen e esqueleto externo (exoesqueleto) rico em quitina conferem características próprias desses animais. Em determinados momentos, o exoesqueleto antigo é substituído por um novo – fenômeno denominado muda, permitindo o crescimento do indivíduo.
Os indivíduos possuem tubo digestivo completo; sistema respiratório, com respiração traqueal ou branquial e excreção por tubos de Malpighi, na maioria deles.
Os artrópodes podem ser classificados usando como critério o número de patas. Abaixo, um quadro comparativo entre as classes mais conhecidas:
- Classe Crustacea: Possuem 5 ou mais pares de patas, 2 pares de antenas e corpo dividido em cefalotórax e abdome. A boca é ventral e possui mandíbulas. Tubo digestivo completo com algumas glândulas anexas, como o hepatopâncreas. Coração dorsal curto e artérias, com hemolinfa circulando, nem sempre, no interior dos vasos (circulação aberta ou lacunar). Sistema excretor com um par de glândulas verdes; aparelho respiratório braquial; pelos tácteis e sistema nervoso ganglionar. Exemplos: lagostas, camarões, cracas, siris, caranguejos, etc.
- Classe Arachnida: Com 4 pares de patas e corpo dividido em cefalotórax e abdome. O sistema digestivo é completo, sistema circulatório aberto e respiração traqueal ou filotraqueal – quando há uma abertura ventral no abdome, que se comunica com os pulmões foliáceos. A excreção se dá por meio de tubos de Malpighi ou por glândulas coxais. São, na maioria dos casos, dioicos com fecundação interna. Exemplos: aranhas, carrapatos, ácaros, opiliões, escorpiões, etc.
- Classe Chilopoda: 15 ou mais pares de patas; trocas gasosas efetuadas por um sistema de traqueias; túbulos de Malpighi. Corpo dividido em cabeça e tronco articulado. São carnívoros. Exemplos: centopeias e lacraias.
- Classe Diplopoda: Possuem de 18 a mais de 750 pares de patas. São dotados de um par de antenas curtas e um par de mandíbulas. São dioicos e a reprodução é sexuada. Exemplos: piolhos de cobra.
- Classe Insecta: 3 pares de patas, 1 par ou 2 pares de asa, ou nenhum, sendo este último o mais comum. 1 par de antenas e corpo dividido em cabeça, tórax e abdome. Possuem olhos compostos. A excreção se dá por tubos de Malpighi, liberando, principalmente, ácido úrico. A fecundação é interna, marcada por estágios larvais e metamorfose. Há algumas formas especiais de reprodução, como partenogênese, pedogênese e poliembrionia. A respiração é traqueal e o sistema nervoso, ganglionar, com cordão nervoso ventral. Exemplos: Borboletas, mosquitos, gafanhotos, etc.
Por Mariana Araguaia
Graduada em Biologia
Equipe Brasil Escola
Ângulos
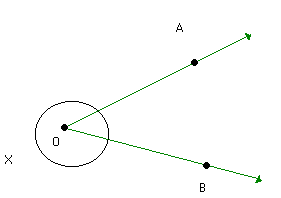
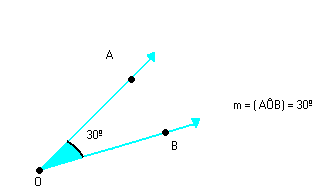
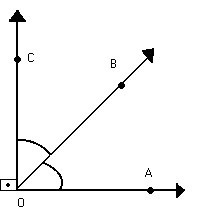
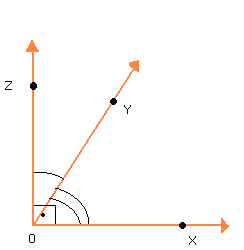
O ÂNGULO E SEUS ELEMENTOS
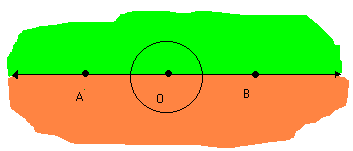
Duas semi-retas que não estejam contidas na mesma reta, e que tenham a mesma origem, dividem o plano em duas regiões: uma convexa e outra não-convexa.
Cada uma dessas regiões, junto com as semi-retas, forma um ângulo. Assim, as duas semi-retas determinam dois ângulos:
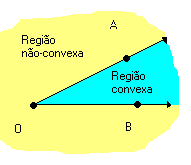
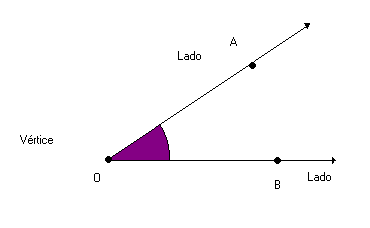
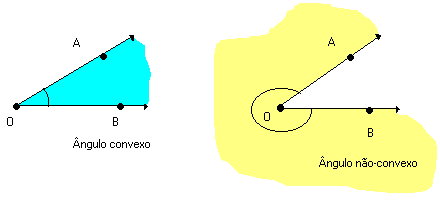 Todo ângulo possui dois lados e um vértice. Os lados são as semi-retas que determinam. O vértice é a origem comum dessas semi-retas.
Todo ângulo possui dois lados e um vértice. Os lados são as semi-retas que determinam. O vértice é a origem comum dessas semi-retas.
O ângulo convexo, de vértice O e lados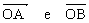 , é indicado por: AÔB, BÔA ou Ô.
, é indicado por: AÔB, BÔA ou Ô.
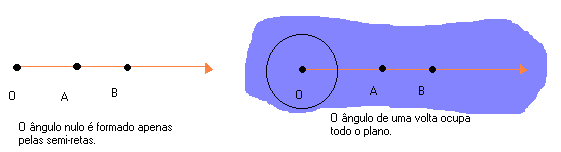
 Observe agora dois casos em que as semi-retas de mesma origem estão contidas na mesma reta. Nesses casos, formam-se também ângulos.
Observe agora dois casos em que as semi-retas de mesma origem estão contidas na mesma reta. Nesses casos, formam-se também ângulos.
MEDIDA DE UM ÂNGULO
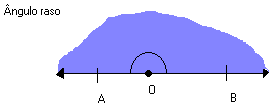
A medida de um ângulo é dada pela medida de sua abertura. A unidade padrão de medida de um ângulo é o grau, cujo símbolo é º.
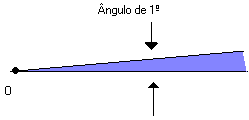
Tomando um ângulo raso ou de meia-volta e dividindo-o em 180 partes iguais, determinamos 180 ângulos de mesma medida. Cada um desses ângulos representa um ângulo de 1º grau (1º).
 Para medir ângulos utilizamos um instrumento denominado transferidor. O transferidor já vem graduado com divisões de 1º em 1º. Existem dois tipos de transferidor: Transferidor de 180º e de 360º.
Para medir ângulos utilizamos um instrumento denominado transferidor. O transferidor já vem graduado com divisões de 1º em 1º. Existem dois tipos de transferidor: Transferidor de 180º e de 360º.
O grau compreende os submúltiplos:
Logo, podemos concluir que:
Quando um ângulo é medido em graus, minutos e segundos, estamos utilizando o sistema sexagesimal.
Como medir um ângulo, utilizando o transferidor
Observe a seqüência
Observe as seguintes indicações de ângulos e suas respectivas leituras:
15º (lê-se "15 graus'')
45º50' (lê-se ''45 graus e 50 minutos'')
30º48'36'' (lê-se ''30 graus, 48 minutos e 36 segundos'')
Observações
Além do transferidor, existem outros instrumentos que medem ângulos com maior precisão. Como exemplos temos o teodolito, utilizado na agrimensura, e o sextante, utilizado em navegação.
A representação da medida de um ângulo pode também ser feita através de uma letra minúscula ou de um número.

Um ângulo raso ou de meia-volta mede 180º.
O ângulo de uma volta mede 360º.
Questões envolvendo medidas de ângulos
Observe a resolução das questões abaixo:
 Solução
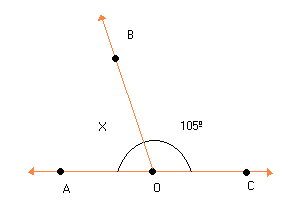
Solução
Medida de AÔB = x
Medida de BÔC = 105º
Como m ( AÔC) é 180º, pois é um ângulo raso, temos:
m (AÔB) + m (BÔC) = m (AÔC)
x + 105º = 180º
x = 180º - 105º
x = 75º
Logo, a medida de AÔB é 75º.
 Solução
Solução
Verificamos que o ângulo não-convexo na figura (x) e o ângulo convexo (50º) formam, juntos, um ângulo de uma volta, que mede 360º. Assim:

Medidas fracionárias de um ângulo
Subtração
Observe os exemplos:
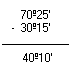
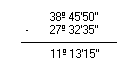
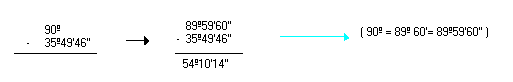
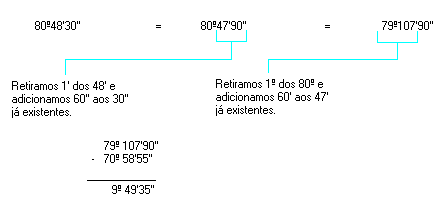
Logo, a diferença é 9º 49'35''.
Multiplicação por um número natural
Observe os exemplos:
Divisão por um número natural
Observe os exemplos:
ÂNGULOS CONGRUENTES
Observe os ângulos abaixo:
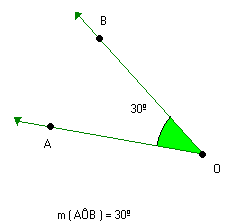
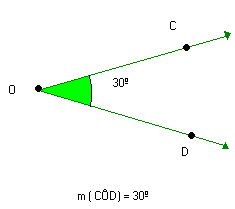 Verifique que AÔB e CÔD têm a mesma medida. Eles são ângulos congruentes e podemos fazer a seguinte indicação:
Verifique que AÔB e CÔD têm a mesma medida. Eles são ângulos congruentes e podemos fazer a seguinte indicação:
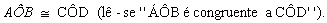
Assim:
Propriedades da Congruência
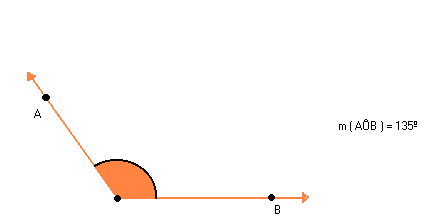
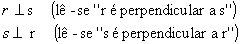
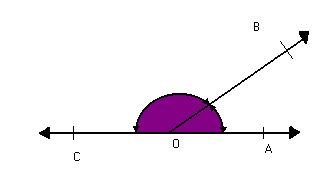
Exemplo:
Os ângulos que medem 82º e 98º são suplementares, pois 82º + 98º = 180º.
Dizemos que o ângulo de 82º é o suplemento do ângulo de 98º, e vice-versa.
Para calcular a medida do suplemento de um ângulo, devemos determinar a diferença entre 180º e a medida do ângulo agudo dado.
Exemplo:
Medida do suplemento = 180º - medida do ângulo
Medida do suplemento = 180º - 55º
Medida do suplemento = 125º
Logo, a medida do suplemento do ângulo de 55º é 125º.
Observação:
www.somatematica.com.br
Duas semi-retas que não estejam contidas na mesma reta, e que tenham a mesma origem, dividem o plano em duas regiões: uma convexa e outra não-convexa.
Cada uma dessas regiões, junto com as semi-retas, forma um ângulo. Assim, as duas semi-retas determinam dois ângulos:


O ângulo convexo, de vértice O e lados


- As semi-retas
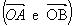 coincidem. Temos aí o ângulo nulo e o ângulo de uma volta.
coincidem. Temos aí o ângulo nulo e o ângulo de uma volta.

- As semi-retas
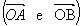 não coincidem. Temos aí dois ângulos rasos ou de meia-volta.
não coincidem. Temos aí dois ângulos rasos ou de meia-volta.

Podemos, então, estabelecer que:
| Ângulo é a região do plano limitada por duas semi-retas que têm a mesma origem. |
A medida de um ângulo é dada pela medida de sua abertura. A unidade padrão de medida de um ângulo é o grau, cujo símbolo é º.
Tomando um ângulo raso ou de meia-volta e dividindo-o em 180 partes iguais, determinamos 180 ângulos de mesma medida. Cada um desses ângulos representa um ângulo de 1º grau (1º).


O grau compreende os submúltiplos:
- O minuto corresponde a
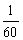 do grau. Indica-se um minuto por 1'.
do grau. Indica-se um minuto por 1'.
| 1º=60' |
- O segundo corresponde a
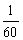 do minuto. Indica-se um segundo por 1''.
do minuto. Indica-se um segundo por 1''.
| 1'=60'' |
1º = 60'.60 = 3.600''
|
Como medir um ângulo, utilizando o transferidor
Observe a seqüência
- O centro O do transferidor deve ser colocado sobre o vértice do ângulo.
- A linha horizontal que passa pelo centro deve coincidir com uma das semi-retas do ângulo
 .
. - Verificamos a medida da escala em que passa a outra semi-reta
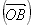 .
.
Observe as seguintes indicações de ângulos e suas respectivas leituras:
15º (lê-se "15 graus'')
45º50' (lê-se ''45 graus e 50 minutos'')
30º48'36'' (lê-se ''30 graus, 48 minutos e 36 segundos'')
Observações
Além do transferidor, existem outros instrumentos que medem ângulos com maior precisão. Como exemplos temos o teodolito, utilizado na agrimensura, e o sextante, utilizado em navegação.
A representação da medida de um ângulo pode também ser feita através de uma letra minúscula ou de um número.

Um ângulo raso ou de meia-volta mede 180º.
O ângulo de uma volta mede 360º.
Questões envolvendo medidas de ângulos
Observe a resolução das questões abaixo:
- Determine a medida do ângulo AÔB na figura:

Medida de AÔB = x
Medida de BÔC = 105º
Como m ( AÔC) é 180º, pois é um ângulo raso, temos:
m (AÔB) + m (BÔC) = m (AÔC)
x + 105º = 180º
x = 180º - 105º
x = 75º
Logo, a medida de AÔB é 75º.
- Determine a medida do 6angulo não-convexo na figura:

Verificamos que o ângulo não-convexo na figura (x) e o ângulo convexo (50º) formam, juntos, um ângulo de uma volta, que mede 360º. Assim:
x + 50º = 360º
x = 360º - 50º
x = 310º
Logo, o valor do ângulo não-convexo é 310º.
Como construir um ângulo utilizando o transferidor
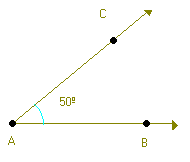
Observe a seqüência utilizada na construção de um ângulo de 50º:
- Traçamos uma semi-reta
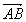 .
.

- Colocamos o centro do transferidor sobre a origem da semi-reta (A).
- Identificamos no transferidor o ponto (C) correspondente à medida de 50º.

- Traçamos a semi-reta
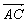 , obtendo o ângulo BÂC que mede 50º.
, obtendo o ângulo BÂC que mede 50º.
Os ângulos de 30º, 45º, 60º e 90º são ângulos especiais.
Eles podem ser desenhados com esquadro.
TRANSFORMAÇÃO DE UNIDADES
Como vimos, quando trabalhamos com medidas de ângulos, utilizamos o sistema sexagesimal.
Observe nos exemplos como efetuar transformações nesse sistema:
- Transforme 30º em minutos.
Solução
Sendo 1º = 60', temos:
30º = 30 . 60'= 1.800
'Logo, 30º = 1.800
- Transforme 5º35' em minutos.
Solução
5º = 5 . 60' = 300'
300' + 35'= 335'
Logo, 5º35'= 335'.
- transforme 8º em segundos.
Solução
Sendo 1º = 60', temos:
8º = 8 . 60'= 480
'Sendo 1'= 60'', temos:
480'= 480 . 60'' = 28.800''
Logo, 8º = 28.800''.
- Transforme 3º35' em segundos.
Solução
3º = 3 . 60'= 180'
180' + 35' = 215'
215' . 60'' = 12.900''
Logo, 3º35'= 12.900''
- Transforme 2º20'40'' em segundos.
Solução
2º = 2 . 60' = 120'
120' + 20' = 140'
140'. 60''= 8.400''
8.400'' + 40'' = 8.440''
Logo, 2º20'40'' = 8.440''
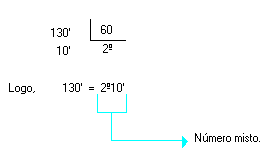
Transformando uma medida de ângulo em número misto
- Transforme 130' em graus e minutos.
Solução

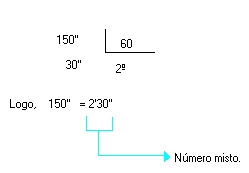
- Transforme 150'' em minutos e segundos.
Solução

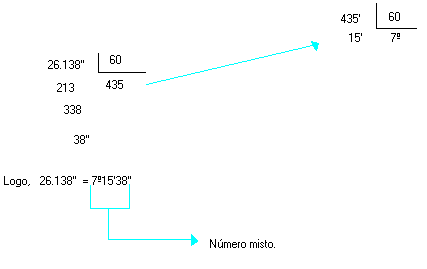
- Transforme 26.138'' em graus, minutos e segundos.
Solução

Medidas fracionárias de um ângulo
- Transforme 24,5º em graus e minutos.
solução
0,5º = 0,5 . 60' = 30'
24,5º= 24º + 0,5º = 24º30'
Logo, 24,5º = 24º30'.
- Transforme 45º36' em graus.
solução
60'  1º
1º
36'  x
x 
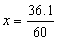
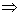
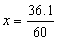
x = 0,6º (lê-se ''seis décimos de grau'')
Logo, 45º36'= 45º + 0,6º = 45,6º.
- Transforme 5'54'' em minutos.
Solução
60'' 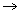 1'
1'
54'' 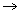 x
x 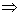
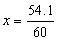
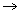 x
x 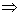
x = 0,9' ( lê-se ''nove décimos de minuto'')
Logo, 5'54'' = 5'+ 0,9'= 5,9'
OPERAÇÕES COM MEDIDAS DE ÂNGULOS
Observe alguns exemplos de como adicionar medidas de ângulos:
Adição
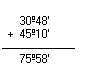 |
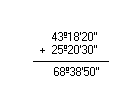 |
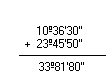 Simplificando 33º81'80'', obtemos: 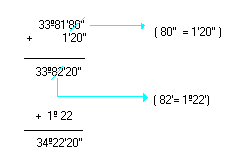 Logo, a soma é 34º22'20''. | |
Observe os exemplos:
- 70º25' - 30º15
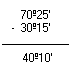
- 38º45'50'' - 27º32'35''
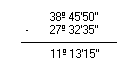
- 90º - 35º49'46''
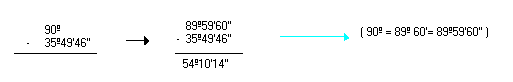
- 80º48'30'' - 70º58'55''

Logo, a diferença é 9º 49'35''.
Multiplicação por um número natural
Observe os exemplos:
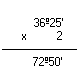 |
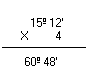 |
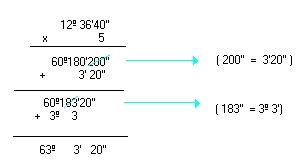 Logo, o produto é 63º3'20''. | |
Observe os exemplos:
|
|
|
ÂNGULOS CONGRUENTES
Observe os ângulos abaixo:


Assim:
| Dois ângulos são congruentes quando têm a mesma medida. |
- Reflexiva:
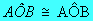
- Simétrica:

- Transitiva:
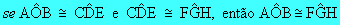
- ÂNGULOS CONSECUTIVOSObserve a figura:
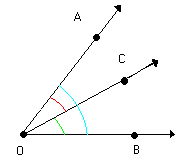
Nela identificamos os ângulos AÔC, CÔB e AÔB.Verifique em cada uma das figuras abaixo que: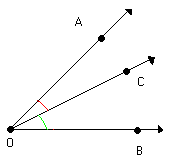
Os ângulos AÔC e CÔB possuem:
Vértice comum: O
Lado comum:
Os ângulos AÔC e AÔB possuem:
Vértice comum: O
Lado comum: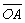
Os ângulos CÔB e AÔB possuem:
Vértice comum: O
Lado comum: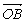 Os pares de ângulos AÔC e CÔB, AÔC e AÔB, CÔB e AÔB são denominados ângulos consecutivos.Assim:Dois ângulos são consecutivos quando possuem o mesmo vértice e um lado comum.
Os pares de ângulos AÔC e CÔB, AÔC e AÔB, CÔB e AÔB são denominados ângulos consecutivos.Assim:Dois ângulos são consecutivos quando possuem o mesmo vértice e um lado comum. - ÂNGULOS ADJACENTES
Observe os exemplos de ângulos consecutivos vistos anteriormente e verifique que:
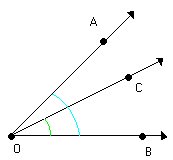
Os ângulos AÔC e CÔB não possuem pontos internos comuns 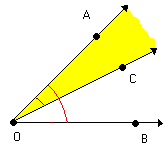
Os ângulos AÔC e AÔB possuem pontos internos comuns 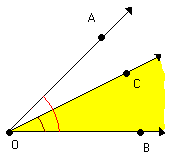
Os ângulos CÔB e AÔB possuem pontos internos comuns
Verifique que os ângulos AÔC e CÔB são consecutivos e não possuem pontos internos comuns. Por isso eles são denominados ângulos adjacentes.
Assim:
Dois ângulos são adjacentes quando são consecutivos e não possuem pontos internos comuns.
Observação:
Duas retas concorrentes determinam vários ângulos adjacentes. Exemplos:
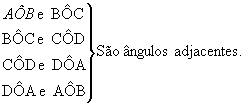
- BISSETRIZ DE UM ÂNGULO
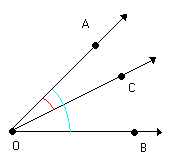
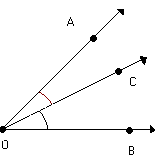
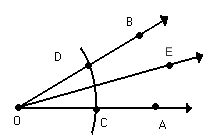
Observe a figura abaixo:
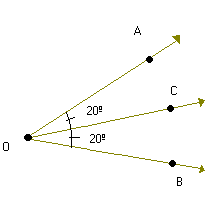 m ( AÔC ) = m (CÔB ) = 20º
m ( AÔC ) = m (CÔB ) = 20º
Verifique que a semi-reta divide o ângulo AÔB em dois ângulos ( AÔB e CÔB ) congruentes.
divide o ângulo AÔB em dois ângulos ( AÔB e CÔB ) congruentes.
Nesse caso, a semi-reta é denominada bissetriz do ângulo AÔB.
é denominada bissetriz do ângulo AÔB.
Assim:
Bissetriz de um ângulo é a semi-reta com origem no vértice desse ângulo e que o divide em dois outros ângulos congruentes. Utilizando o compasso na construção da bissetriz de um ânguloDeterminação da bissetriz do ângulo AÔB.- Centramos o compasso em O e com uma abertura determinamos os pontos C e D sobre as semi-retas
 , respectivamente.
, respectivamente.
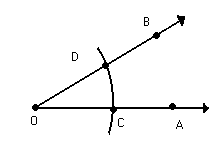
- Centramos o compasso em C e D e com uma abertura superior à metade da distância de C a D traçamos arcos que se cruzam em E.
- Traçamos
 , determinando assim a bissetriz de AÔB.
, determinando assim a bissetriz de AÔB.
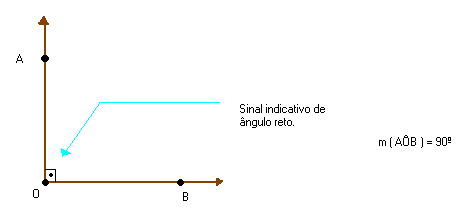
 ÂNGULO AGUDO, OBTUSO E RETOPodemos classificar um ângulo em agudo, obtuso ou reto.
ÂNGULO AGUDO, OBTUSO E RETOPodemos classificar um ângulo em agudo, obtuso ou reto. - Centramos o compasso em O e com uma abertura determinamos os pontos C e D sobre as semi-retas
- Ângulo agudo é o ângulo cuja medida é menor que 90º. Exemplo:

- Ângulo obtuso é o ângulo cuja medida é maior que 90º. Exemplo:
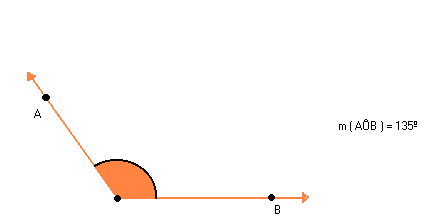
- Ângulo reto é o ângulo cuja medida é 90º. Exemplo:

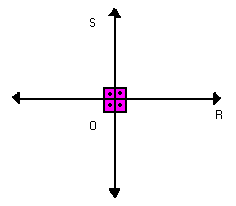
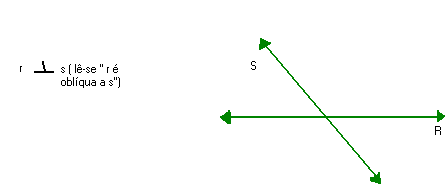
RETAS PERPENDICULARES
As retas r e s da figura abaixo são concorrentes e formam entre si quatro ângulos retos.

Dizemos que as retas r e s são perpendiculares e indicamos:
Observação
Duas retas concorrentes que não formam ângulos retos entre si são chamadas de oblíquos. Exemplo:

ÂNGULOS COMPLEMENTARES
Observe os ângulos AÔB e BÔC na figura abaixo:

Verifique que:
m (AÔB) + m (BÔC) = 90º
Nesse caso, dizemos que os ângulos AÔB e BÔC são complementares.
Assim:
Dois ângulos são complementares quando a soma de suas medidas é 90º.
|
Exemplo:
Os ângulos que medem 42º e 48º são complementares, pois 42º + 48º = 90º.
Dizemos que o ângulo de 42º é o complemento do ângulo de 48º, e vice-versa.
Para calcular a medida do complemento de um ângulo, devemos determinar a diferença entre 90º e a medida do ângulo agudo dado.
| Medida do ângulo | Complemento |
| x | 90º - x |
Exemplo:
- Qual a medida do complemento de um ângulo de 75º?
Solução
Medida do complemento = 90º - medida do ângulo
Medida do complemento = 90º - 75º
Medida do complemento = 15º
Logo, a medida do complemento do ângulo de 75º é 15º.
Observação:
Os ângulos XÔY e YÔZ da figura ao lado, além de complementares, são também adjacentes. Dizemos que esses ângulos são adjacentes complementares.

ÂNGULOS SUPLEMENTARES
Observe os ângulos AÔB e BÔC na figura abaixo:
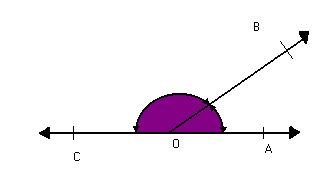
As semi-retas  formam um ângulo raso.
formam um ângulo raso.
 formam um ângulo raso.
formam um ângulo raso.
Verifique que:
m ( AÔB ) + m (BÔC) = 180º
Nesse caso, dizemos que os ângulos AÔB e BÔC são suplementares. Assim:
Dois ângulos são suplementares quando a soma de suas medidas é 180º.
|
Os ângulos que medem 82º e 98º são suplementares, pois 82º + 98º = 180º.
Dizemos que o ângulo de 82º é o suplemento do ângulo de 98º, e vice-versa.
Para calcular a medida do suplemento de um ângulo, devemos determinar a diferença entre 180º e a medida do ângulo agudo dado.
| Medida do ângulo | Suplemento |
| X | 180º - X |
- Qual a medida do suplemento de um ângulo de 55º?
Medida do suplemento = 180º - medida do ângulo
Medida do suplemento = 180º - 55º
Medida do suplemento = 125º
Logo, a medida do suplemento do ângulo de 55º é 125º.
Observação:
| Os ângulos XÔY e YÔZ da figura ao lado, além de suplementares, são também adjacentes. Dizemos que esses ângulos são adjacentes suplementares. | 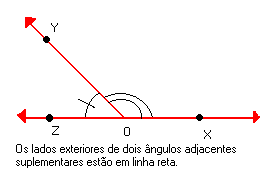 |
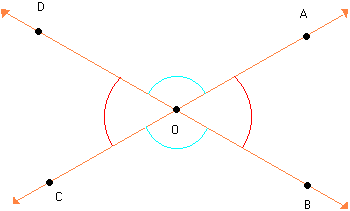
- ÂNGULOS OPOSTOS PELO VÉRTICE
Observe os ângulos AÔB e CÔD na figura abaixo:
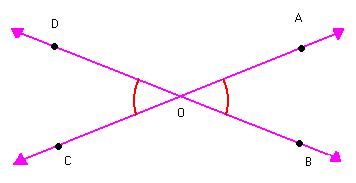 Verifique que:
Verifique que: Nesse caso, dizemos que os ângulos AÔB e CÔD são opostos pelo vértice (o.p.v). Assim:
Nesse caso, dizemos que os ângulos AÔB e CÔD são opostos pelo vértice (o.p.v). Assim:Dois ângulos são opostos pelo vértice quando os lados de um deles são semi-retas opostas aos lados do outro. Na figura abaixo, vamos indicar: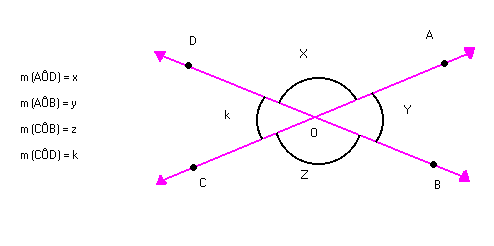 Sabemos que:X + Y = 180º ( ângulos adjacentes suplementares)X + K = 180º ( ângulos adjacentes suplementares)Então:
Sabemos que:X + Y = 180º ( ângulos adjacentes suplementares)X + K = 180º ( ângulos adjacentes suplementares)Então: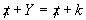 Logo: y = kAssim:m (AÔB) = m (CÔD)
Logo: y = kAssim:m (AÔB) = m (CÔD)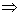 AÔB
AÔB 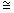 CÔDm (AÔD) = m (CÔB)
CÔDm (AÔD) = m (CÔB)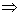 AÔD
AÔD 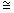 CÔBDaí a propriedade:Dois ângulos opostos pelo vértice são congruentes.
CÔBDaí a propriedade:Dois ângulos opostos pelo vértice são congruentes.
Observe uma aplicação dessa propriedade na resolução de um problema:
- Dois ângulos opostos pelo vértice têm medidas, em graus, expressas por x + 60º e 3x - 40º. Qual é o valor de x?
| x + 60º = 3x - 40º x - 3x = - 40º - 60º -2x = - 100º x = 50º Logo, o valor de x é 50º. | 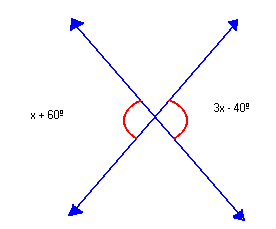 |
Assinar:
Comentários (Atom)