Parábola

. Parábola

Definição

Considerando um ponto F (foco) e uma reta d (diretriz), sendo F ∉ d, pertencentes a um mesmo plano, definimos parábola como o lugar geométrico dos pontos P do plano eqüidistante do ponto F e da reta d.

PF = Pd

Elementos principais



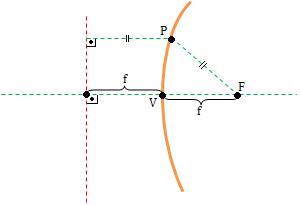
F é o foco
d é a diretriz
V é o vértice
p = 2 . f é o parâmetro (FV = Vd = f)
é o eixo das simetrias

Equação reduzida

Suponha a parábola da figura: eixo de simetria contido no eixo “x” e vértice na origem.



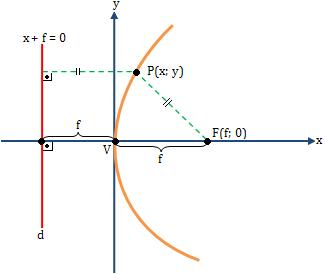
Referente ao sistema de eixos cartesianos, temos:

Foco: F(f; 0)
Diretriz: x = -f

Supondo P(x; y) como um ponto genérico da parábola, da definição PF = PD, resulta:



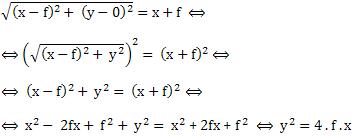
A equação: y² = 4 . f . x

chamada de equação reduzida da parábola com eixo de simetria contido no eixo “x” e vértice na origem, quando a hipérbole estiver voltada para a direita.

Quando a parábola estiver voltada para a esquerda, sua equação reduzida será:

y² = – 4 . f . x

Excentricidade

A excentricidade na parábola é a razão:

www.colegioweb.com.br