Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
Na matemática, o limite tem o objetivo de determinar o comportamento de uma função à medida que ela se aproxima de alguns valores, sempre relacionando os pontos x e y. Utilizando a função y = x + 1, vamos determinar os valores de y à medida que x assume alguns valores. Veja:
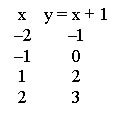
Note que à medida que x se aproxima de –2, o valor de y se aproxima de –1, isto é, quando x tende a –2 (x → –2), y tende a –1 (y → –1). Portanto:
x → –1, y → 0
x → 1, y → 2
x → 2, y → 3
A utilização de limites ajuda na compreensão de diversas situações envolvendo funções, através de pontos notáveis como mínimo e máximo ou até mesmo os pontos de intersecção entre funções, a continuidade de funções também utiliza as noções de limites, bem como os problemas envolvendo séries numéricas convergentes ou divergentes.
Vamos trabalhar a função f(x) = x², mostrando que à medida que os valores de x aproximam de 3, pela esquerda ou pela direita, a função se aproxima do valor 9.
Pela direita
f(3,1) = (3,1)² = 9,61
f(3,01) = (3,01)² = 9,06
f(3,001) = (3,001)² = 9,006001
f(3,0001) = (3,0001)² = 9,00060001
Pela esquerda
f(2,9) = (2,9)² = 8,41
f(2,99) = (2,99)² = 8,9401
f(2,999) = (2,999)² = 8,994001
f(2,9999) = (2,9999)² = 8,99940001
Observe que à medida que os valores se aproximam de 3, tanto pela direita quanto pela esquerda, a imagem da função f(x) = x², fica mais próxima do valor 8.
Exemplo 1
Dada a função f(x) = 4x + 1, determine a sua imagem à medida que o valor de x tende a 2.
f(x) = 4x + 1 f(2) = 4 * 2 + 1 f(2) = 9
Exemplo 2
Vamos determinar o limite da função f(x) = x² – 5x + 3, quando x tende a 4.
Nesse caso devemos aplicar a seguinte regra: o limite das somas é a soma dos limites. Portanto, devemos determinar o limite de cada monômio e depois realizar a soma entre eles.
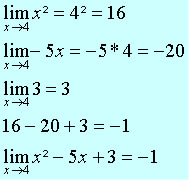
Exemplo 3Calcular o limite da função
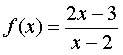, quando x tende a –2.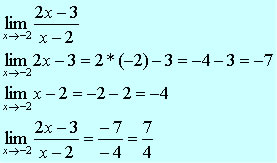 
Exemplo 4Determine o limite da função
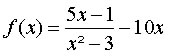, à medida que x se aproxima de 1.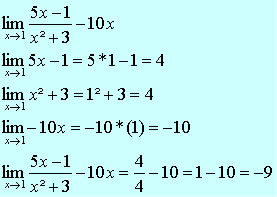 
Nenhum comentário:
Postar um comentário