Inequação Produto

Algumas inequações apresentam, no 1º membro, produto de funções que para obter a resolução dessas inequações é preciso fazer o estudo do sinal de todas as funções, a solução seria a intersecção do estudo dos sinais das funções que pertencem à inequação.

Para compreender melhor como funciona o encontro do conjunto solução de uma inequação produto acompanhe o raciocínio dos exemplos seguintes.

Exemplo 1:

Ache o conjunto solução da equação produto abaixo:
(-3x + 6) (5x -7) < 0

Primeiro o estudo do sinal de cada função:
-3x + 6 = 0
-3x = -6
-x = - 6 : (3)
-x = - 2
x = 2



5x – 7 = 0
5x = 7
x = 7 5




Fazendo o jogo de sinal com o estudo de sinal em cada coluna formada por uma função:


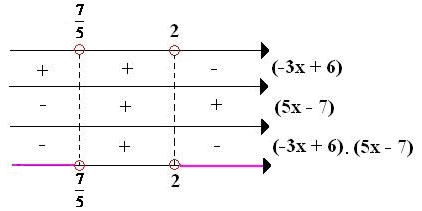
Como a inequação quer valores que sejam menores que 0 escrevemos que o conjunto solução da inequação será:

S = {x R / x < 7 ou x > 2}
5
Exemplo 2:

Ache o conjunto solução da equação produto abaixo:
(2x – 10) (x² – 5x + 6) > 0

Primeiro o estudo do sinal de cada função:
2x – 10 = 0
2x = 10
x = 10 : 2
x = 5



x2 – 5x + 6 = 0
∆ = 25 – 4 . 1 . 6
∆ = 25 – 24
∆ = 1

x = 5 ± 1
2

x’ = 3
x” = 2



Fazendo o jogo de sinal com o estudo de sinal em cada coluna formada por uma função:



Como a inequação quer valores que sejam maiores que 0 escrevemos que o conjunto solução da inequação (2x – 10) (x2 – 5x + 6) > 0, será:

S = {x R / 2 < x < 3 ou x > 5}

Exemplo 3:

x . (x – 1) (-x + 2) ≤ 0

x = 0


x – 1 = 0
x = 1


-x + 2 = 0
-x = -2
x = 2


Fazendo o jogo de sinal com o estudo de sinal em cada coluna formada por uma função:


Como a inequação quer valores que sejam menores ou iguais a 0 escrevemos que o conjunto solução da inequação
x . (x – 1) (-x + 2) ≤ 0, será:

{x R / 0 ≤ x ≤ 1 ou x ≥ 2}.
Danielle de Miranda