Equações trigonométricas

Professor de Matemática e Biologia Antônio Carlos Carneiro Barroso

Colégio Estadual Dinah Gonçalves

email accbarroso@hotmail.com

 www.ensinodematemtica.blogspot.com.br

www.accbarrosogestar.blogspot.com.br 

        

Equações Trigonométricas

INTRODUÇÃO

Quando encontramos função trigonométrica da incógnita ou função trigonométrica de alguma função da incógnita em pelo menos um dos membros de uma equação, dizemos que esta equação é trigonométrica.

Exemplos:
1) sen x + cos x =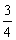 e sen 2x = cos² x são equações trigonométricas.

2) x + ( tg 30º) . x² e x + sen 60º = 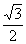não são equações trigonométricas.

Dizemos que r é uma raiz ou solução da equação trigonométrica f(x) = g(x) se r for elemento do domínio de f e g e se f(r) = g(r) for verdadeira.

Na equação sen x - sen =0, por exemplo, os números são algumas de suas raízes e os números não o são.

O conjunto S de todas as raízes da equação é o seu conjunto solução ou conjunto verdade.

Quase todas as equações trigonométricas, quando convenientemente tratadas e transformadas, podem ser reduzidas a pelo menos uma das três equações seguintes:

sen x = sen a

cos x = cos a

tg x = tg a

Estas são as equações trigonométricas elementares ou equações trigonométricas fundamentais.

RESOLUÇÃO DA 1ª EQUAÇÃO FUNDAMENTAL

Ela baseia-se no fato de que, se dois arcos têm o mesmo seno, então eles são côngruos ou suplementares.

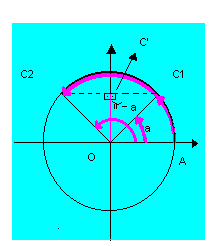
Logo, podemos escrever que:

sen x = sen a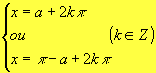

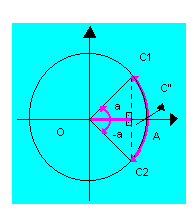
O conjunto solução dessa equação será, portanto:

Logo, podemos escrever que:

cos x = cos a x = a +

O conjunto solução dessa equação será, portanto:

RESOLUÇÃO DA 3ª EQUAÇÃO FUNDAMENTAL

Ela baseia-se no fato de que, se dois arcos têm a mesma tangente, então eles são côngruos ou têm suas extremidades simétricas em relação ao centro do ciclo trigonométrico.

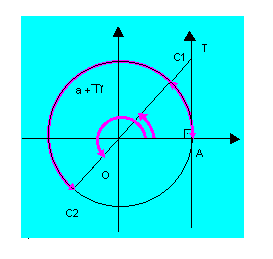
Logo, podemos escrever que:

O conjunto solução dessa equação será, portanto:

www.somatematica.com.br