Matriz transposta e matriz simétrica

Marcelo Rigonatto

Transposta de uma matriz

Considere uma matriz A =(a_ij)_{(m x n)}. A matriz transposta de A, representada por A^t, é uma matriz da forma A^t = (b_ji)_{(n x m)}, tal que:
b_ji = a_ij

Observe que a matriz A é de ordem m x n, enquanto A^t é de ordem n x m. Essa “inversão” das ordens das duas matrizes se deve ao fato de que para obter a transposta de A devemos “transformar” cada uma de suas linhas em colunas. De forma simples, é isso o que diz a definição de transposta de uma matriz.

Vejamos alguns exemplos para melhor entendimento.

Exemplo 1. Determine a matriz transposta de cada uma das seguintes matrizes.

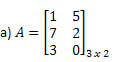
Solução: Para obter a transposta de A, basta “transformar” cada uma de suas linhas em colunas. Assim, teremos:

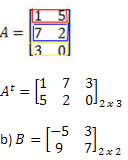
Solução: “Transformando” linha em coluna, obtemos:

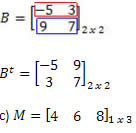
Solução: Nesse caso, teremos:


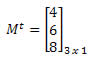
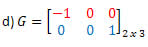
Solução: “Transformando” as linhas em coluna, obtemos:

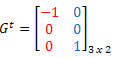
Matriz Simétrica.

Dizemos que uma matriz quadrada A de ordem n é simétrica quando ela for igual à sua transposta. Ou seja, A é denominada simétrica se:

A = A^t

Observe que somente matrizes quadradas podem ser simétricas.

Vejamos alguns exemplos.

Exemplo 2. Determine a transposta de cada matriz a seguir:

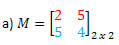
Solução: A transposta de M será obtida “transformando” cada linha de M em coluna. Assim, teremos:

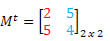
Como M = M^t, dizemos que M é uma matriz simétrica.

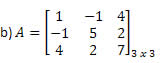
Solução: Vamos obter a transposta de A transformando cada uma de suas linhas em colunas. Assim, teremos:

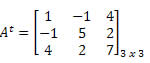
Como A = A^t, dizemos que A é uma matriz simétrica.

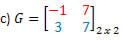
Solução: A transposta de G será a matriz:

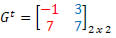
Nesse caso, apesar da matriz G ser quadrada de ordem 2, ela não é igual à sua transposta, portanto não é uma matriz simétrica.

Observação: É fácil notar que (A^t)^t = A.