Professor de Matemática no Colégio Estadual Dinah Gonçalves
E Biologia na rede privada de Salvador-Bahia
Professor Antonio Carlos carneiro Barroso
email accbarroso@hotmail.com
Blog HTTP://ensinodematemtica.blogspot.com e HTTP://accbarroso60.wordpress.com
http://accbarrosogestar.blogspot.com.br
http://accbarrosogestar.blogspot.com.br
Binômio de Newton
Por Marcelo Rigonatto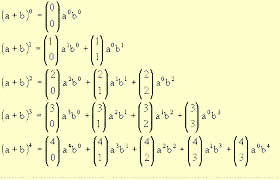
Binômio de Newton
De uma forma geral, quando o expoente é n podemos escrever a fórmula do desenvolvimento do Binômio de Newton da seguinte forma:
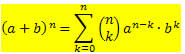
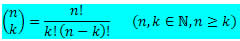
Vejamos alguns exemplos para melhor compreensão.
Exemplo 1. Desenvolva o binômio (a + 2)5.
Solução:
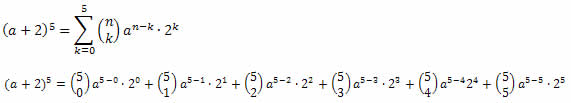
Temos que:
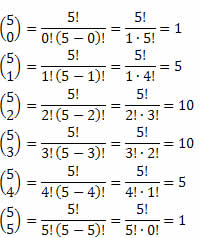
Assim, obtemos:
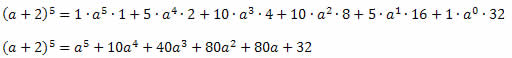
Exemplo 2. Desenvolva o binômio (x + 5)4.
Solução: Utilizando o binômio de Newton, obtemos:
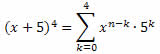
Segue que:
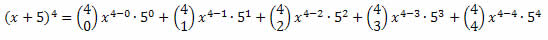
Assim, teremos:
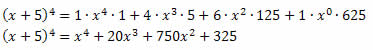
Nenhum comentário:
Postar um comentário