Colégio Estadual Dinah Gonçalves
Seno, cosseno e tangente do arco duplo
Marcelo Rigonatto
Identidades trigonométricas
Dadas as funções circulares de um arco x, é possível, mediante aplicação das fórmulas deduzidas, encontrarmos as funções circulares dos arcos 2x, 3x, ..., chamados, respectivamente, de arco duplo, arco triplo...
Vejamos as expressões que determinam o seno, o cosseno e a tangente do arco duplo. Para isso, faremos 2x = x + x.
1. Seno do arco duplo.
Temos que:
sen2x = sen (x + x)
Utilizando a fórmula do seno da soma de dois arcos, obtemos:
sen 2x = sen (x + x) = senx∙cosx + senx∙cosx
Então:
sen 2x = 2senx∙cosx
2. Cosseno do arco duplo
Também utilizando a fórmula do cosseno da soma de dois arcos, obtemos:
cos2x = cos(x + x) = cosx∙cosx - senx∙senx
Ou
cos2x = cos2 x - sen2 x
3. Tangente do arco duplo
Temos que:

Essas fórmulas são úteis para a simplificação de expressões envolvendo relações trigonométricas. Vejamos alguns exemplos para melhor compreensão.
Exemplo. Sabendo que sen x = 12/13 e cos x = 5/13, determine o valor de sen 2x e cos 2x.
Solução: Primeiro vamos determinar o valor de sen 2x. Como conhecemos os valores de sen x e cos x, basta aplicar a fórmula do arco duplo. Assim, temos que:
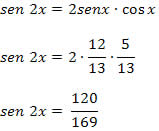
Agora, vamos determinar o valor de cos 2x.
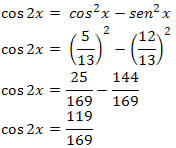
Nenhum comentário:
Postar um comentário