Professor de Matemática no Colégio Estadual Dinah Gonçalves
E Biologia na rede privada de Salvador-Bahia
Professor Antonio Carlos carneiro Barroso
email accbarroso@hotmail.com
Extraído de http://www.alunosonline.com.br
Probabilidade Condicional
Marcelo Rigonatto
Probabilidade Condicional
A probabilidade condicional é dada pela fórmula:

P(A∩B)→é a probabilidade da intersecção de A com B.
P(B)→é a probabilidade de ocorrer o evento B.
A interpretação do enunciado dos problemas relacionados à probabilidade é fundamental para resolução e identificação do tipo de probabilidade a ser calculada. Vejamos alguns exemplos sobre a probabilidade condicional.
Exemplo 1. Em uma urna há um total de 10 bolas, sendo 3 amarelas, 4 azuis e 3 verdes. É retirada uma bola dessa urna, ao acaso, e verifica-se que ela é verde. Qual a probabilidade de se retirar uma bola azul sabendo que a bola verde retirada inicialmente não foi reposta?
Solução: o primeiro passo é identificar os eventos em questão.
Evento A: sair uma bola azul
Evento B: sair uma bola verde
Resolver o exercício consiste em determinar a probabilidade de se retirar uma bola azul da urna sabendo que já foi retirada uma bola verde. Observe que a ocorrência do evento A está condicionada à ocorrência do evento B. Esse é o caso mais simples de problemas envolvendo probabilidade condicional, não sendo necessária a aplicação da fórmula. Veja:
Após a retirada da bola verde, restaram na urna 9 das 10 bolas. Dessas 9 bolas, 4 são azuis. Assim, temos que:
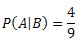
Exemplo 2. Em uma pesquisa realizada com 10.000 consumidores sobre a preferência da marca de sabão em pó, verificou-se que: 6500 utilizam a marca X; 5500 utilizam a marca Y; 2000 utilizam as duas marcas. Foi sorteada uma pessoa desse grupo e verificou-se que ela utiliza a marca X. Qual a probabilidade dessa pessoa ser também usuária da marca Y?
Solução: Vamos identificar cada um dos eventos.
A: Usuário da marca Y.
B: Usuário da marca X.
Queremos determinar P(A|B) e sabemos que o número de elementos do espaço amostral é n(S) = 10000.
Temos, também, que:
n(A∩B) = 2000
Segue que:
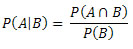
Mas
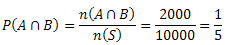
Da teoria de conjunto, temos que:
n(B) = 6500 – n(A∩B) = 6500 – 2000 = 4500
Assim, teremos:
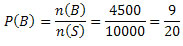
Logo,
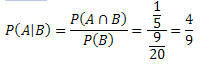
Nenhum comentário:
Postar um comentário