Matrizes

Marcos Noé

Estudo das matrizes

Para organizar dados de uma pesquisa, informações baseadas em números, a Matemática nos fornece um esquema de linhas e colunas denominado Matrizes.
Uma Matriz pode ser representada pelo símbolo aij, onde i: linhas e j: colunas. Toda matriz é disposta na forma m x n, quer dizer uma tabela de m linhas horizontais e n linhas verticais.

Exemplos de matrizes

Matriz 1 x 3 (uma linha e três colunas)

Matriz 2 x 3 (duas linhas e três colunas)

Matriz 3 x 3 (três linhas e três colunas)

Matriz 4 x 4 (quatro linhas e quatro colunas)


Construindo a matriz A = (aij)3x3, em que aij = i + j.

Representação

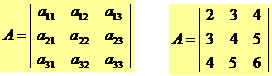
a₁₁ = 1+1 = 2
a₁₂ = 1+2 = 3
a₁₃ = 1+3 = 4
a₂₁ = 2+1 = 3
a₂₂ = 2+2 = 4
a₂₃ = 2+3 = 5
a₃₁ = 3+1 = 4
a₃₂ = 3+2 = 5
a₃₃ = 3+3 = 6


Construindo a matriz A = (aij)_2x3, em que aij = 2i-j.


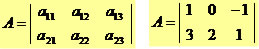
a₁₁ = 2*1 – 1 = 1
a₁₂ = 2*1 – 2 = 0
a₁₃ = 2*1 – 3 = - 1
a₂₁ = 2*2 – 1 = 3
a₂₂ = 2*2 – 2 = 2
a₂₃ = 2*2 – 3 = 1


Casos particulares de matrizes

Matriz linha: possui apenas uma linha



Matriz coluna: possui apenas uma coluna



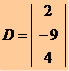
Matriz quadrada: o número de linhas é igual ao número de colunas.