Divisão de polinômio por polinômio

O que vamos relembrar já foi exposto no texto “Divisão de polinômio por monômio”, mas vamos rever novamente: em toda divisão temos o dividendo, divisor, quociente e resto, como estamos falando de divisão de polinômio por polinômio, teremos:

Para o dividendo um polinômio G(x)
Para o divisor um polinômio D(x)
Para o quociente um polinômio Q(x)Para o resto (podendo ser zero) um polinômio R(x)



Prova real:

Tem algumas observações a serem feitas, como:

► ao final da divisão o resto sempre tem que ser menor que o divisor: R(x) < D(x).

► quando o resto for igual a zero, a divisão é considerada exata, ou seja, o dividendo é divisível pelo divisor. R(x) = 0.

Observe a divisão de polinômio por polinômio abaixo, vamos partir de um exemplo, cada passo tomado no desenvolvimento da divisão será explicado.

Dada a divisão
(12x³ + 9 – 4x) : (x + 2x² + 3)

Antes de começar a operação temos que fazer algumas verificações:
► se todos os polinômios estão em ordem conforme as potências de x.

No caso da nossa divisão devemos ordenar, ficando assim:
(12x³ - 4x + 9) : (2x² + x + 3)

► observar se no polinômio G(x) não está faltando algum termo, se estiver devemos completar.

No polinômio 12x³ - 4x + 9 está faltando o termo x², completando ficará, assim:
12x³ + 0x² - 4x + 9

Agora podemos iniciar a divisão:



► G(x) tem 3 termos e D(x) tem 3 termos. Pegamos o 1º termo de G(x) e dividimos pelo 1º termo de D(x): 12x³ : 2x² = 6x, o resultado multiplicará o polinômio 2x² + x + 3 e o resultado dessa multiplicação subtrairemos pelo polinômio 12x³ + 0x² - 4x + 9. Assim teremos:



► R(x) > D(x), podemos dar continuidade à divisão, repetindo o mesmo processo anterior. Achando agora o segundo termo de Q(x).




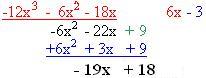
R(x) < D(x), não damos continuidade a divisão, concluindo que:

O quociente é 6x – 3 e o resto é –19x + 18.
Por Danielle de Miranda