Matrizes

Matrizes

Introdução

O crescente uso dos computadores tem feito com que a teoria das matrizes seja cada vez mais aplicada em áreas como Economia, Engenharia, Matemática, Física, dentre outras. Vejamos um exemplo.

A tabela a seguir representa as notas de três alunos em uma etapa:

	Química	Inglês	Literatura	Espanhol
A	8	7	9	8
B	6	6	7	6
C	4	8	5	9

Se quisermos saber a nota do aluno B em Literatura, basta procurar o número que fica na segunda linha e na terceira coluna da tabela.

Vamos agora considerar uma tabela de números dispostos em linhas e colunas, como no exemplo acima, mas colocados entre parênteses ou colchetes:

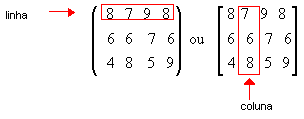
Em tabelas assim dispostas, os números são os elementos. As linhas são enumeradas de cima para baixo e as colunas, da esquerda para direita:

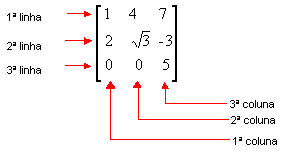
Tabelas com m linhas e n colunas ( m e n números naturais diferentes de 0) são denominadas matrizes m x n. Na tabela anterior temos, portanto, uma matriz 3 x 3.

Veja mais alguns exemplos:

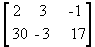• é uma matriz do tipo 2 x 3
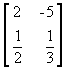• é uma matriz do tipo 2 x 2

Notação geral

Costuma-se representar as matrizes por letras maiúsculas e seus elementos por letras minúsculas, acompanhadas por dois índices que indicam, respectivamente, a linha e a coluna que o elemento ocupa.

Assim, uma matriz A do tipo m x n é representada por:

ou, abreviadamente, A = [a_ij]_{m x n}, em que i e j representam, respectivamente, a linha e a coluna que o elemento ocupa. Por exemplo, na matriz anterior, a₂₃ é o elemento da 2ª linha e da 3ª coluna.

Na matriz 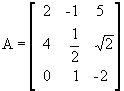, temos:

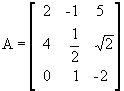Ou na matriz B = [ -1 0 2 5 ], temos: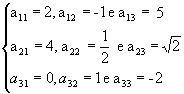 a₁₁ = -1, a₁₂ = 0, a₁₃ = 2 e a₁₄ = 5.

Denominações especiais

Algumas matrizes, por suas características, recebem denominações especiais.

• Matriz linha: matriz do tipo 1 x n, ou seja, com uma única linha. Por exemplo, a matriz A =[4 7 -3 1], do tipo 1 x 4.
  
• Matriz coluna: matriz do tipo m x 1, ou seja, com uma única coluna. Por exemplo,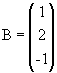, do tipo 3 x 1
  
• Matriz quadrada: matriz do tipo n x n, ou seja, com o mesmo número de linhas e colunas; dizemos que a matriz é de ordem n. Por exemplo, a matriz 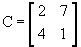é do tipo 2 x 2, isto é, quadrada de ordem 2.

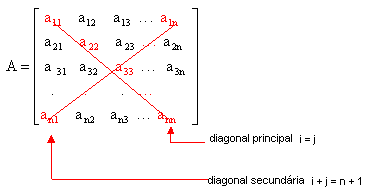
Numa matriz quadrada definimos a diagonal principal e a diagonal secundária. A principal é formada pelos elementos a_ij tais que i = j. Na secundária, temos i + j = n + 1.

Veja:

Observe a matriz a seguir:

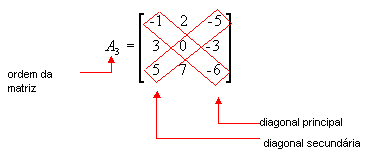
a₁₁ = -1 é elemento da diagonal principal, pis i = j = 1

a₃₁= 5 é elemento da diagonal secundária, pois i + j = n + 1 ( 3 + 1 = 3 + 1)

• Matriz nula: matriz em que todos os elementos são nulos; é representada por 0_{m x n.}

Por exemplo, .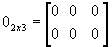

• Matriz diagonal: matriz quadrada em que todos os elementos que não estão na diagonal principal são nulos. Por exemplo:

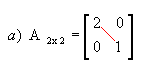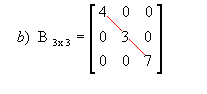• Matriz identidade: matriz quadrada em que todos os elementos da diagonal principal são iguais a 1 e os demais são nulos; é representada por I_n, sendo n a ordem da matriz. Por exemplo:

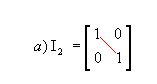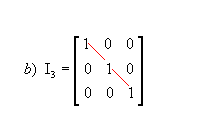Assim, para uma matriz identidade .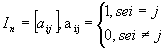

• Matriz transposta: matriz A^t obtida a partir da matriz A trocando-se ordenadamente as linhas por colunas ou as colunas por linhas. Por exemplo:

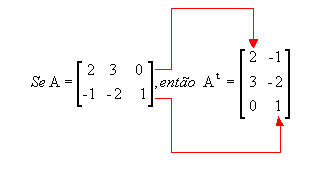
Desse modo, se a matriz A é do tipo m x n, A^t é do tipo n x m.

Note que a 1ª linha de A corresponde à 1ª coluna de A^t e a 2ª linha de A corresponde à 2ª coluna de A^t.

• Matriz simétrica: matriz quadrada de ordem n tal que A = A^t . Por exemplo,

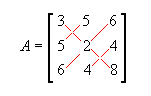é simétrica, pois a₁₂ = a₂₁ = 5, a₁₃ = a₃₁ = 6, a₂₃ = a₃₂ = 4, ou seja, temos sempre a _ij = a _ij.

• Matriz oposta: matriz -A obtida a partir de A trocando-se o sinal de todos os elementos de A. Por exemplo, .

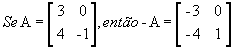Igualdade de matrizes

Duas matrizes, A e B, do mesmo tipo m x n, são iguais se, e somente se, todos os elementos que ocupam a mesma posição são iguais:

.

Operações envolvendo matrizes

Adição

Dadas as matrizes 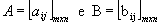, chamamos de soma dessas matrizes a matriz 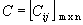, tal que C_ij = a_ij + b_ij , para todo :

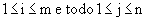A + B = C

Exemplos:

• 
  
• 

Observação: A + B existe se, e somente se, A e B forem do mesmo tipo.

Propriedades

Sendo A, B e C matrizes do mesmo tipo ( m x n), temos as seguintes propriedades para a adição:

a) comutativa: A + B = B + A

b) associativa: ( A + B) + C = A + ( B + C)

c) elemento neutro: A + 0 = 0 + A = A, sendo 0 a matriz nula m x n

d) elemento oposto: A + ( - A) = (-A) + A = 0

Subtração

Dadas as matrizes 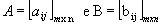, chamamos de diferença entre essas matrizes a soma de A com a matriz oposta de B:

A - B = A + ( - B )

Observe:

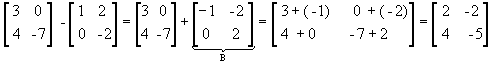
Multiplicação de um número real por uma matriz

Dados um número real x e uma matriz A do tipo m x n, o produto de x por A é uma matriz B do tipo m x n obtida pela multiplicação de cada elemento de A por x, ou seja, b_ij = xa_ij:

B = x.A

Observe o seguinte exemplo:

Propriedades

Sendo A e B matrizes do mesmo tipo ( m x n) e x e y números reais quaisquer, valem as seguintes propriedades:

a) associativa: x . (yA) = (xy) . A

b) distributiva de um número real em relação à adição de matrizes: x . (A + B) = xA + xB

c) distributiva de uma matriz em relação à adição de dois números reais: (x + y) . A = xA + yA

d) elemento neutro : xA = A, para x=1, ou seja, A=A

Multiplicação de matrizes

O produto de uma matriz por outra não é determinado por meio do produto dos sus respectivos elementos.

Assim, o produto das matrizes A = ( a_ij) _{m x p} e B = ( b_ij) _{p x n} é a matriz C = (c_ij) _{m x n} em que cada elemento c_ij é obtido por meio da soma dos produtos dos elementos correspondentes da i-ésima linha de A pelos elementos da j-ésima coluna B.

Vamos multiplicar a matriz 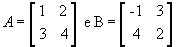para entender como se obtém cada C_ij:

• 1ª linha e 1ª coluna

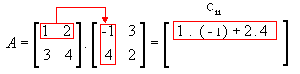
• 1ª linha e 2ª coluna

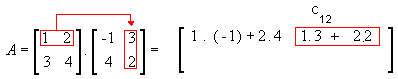
• 2ª linha e 1ª coluna

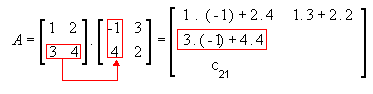
• 2ª linha e 2ª coluna

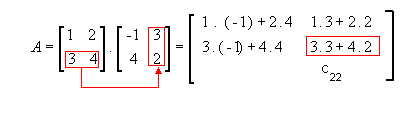
Assim, .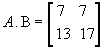

Observe que:

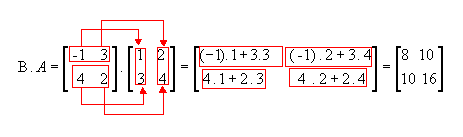
Portanto, 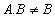.A, ou seja, para a multiplicação de matrizes não vale a propriedade comutativa.

Vejamos outro exemplo com as matrizes :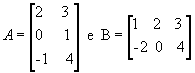

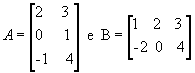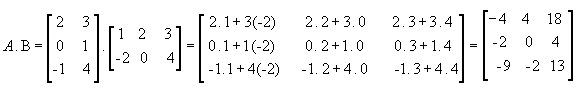
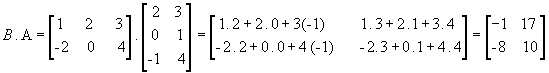
Da definição, temos que a matriz produto A . B só existe se o número de colunas de A for igual ao número de linhas de B:

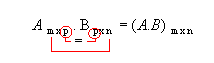
A matriz produto terá o número de linhas de A (m) e o número de colunas de B(n):

• Se A_{3 x 2} e B _{2 x 5} , então ( A . B ) _{3 x 5}
• Se A _{4 x 1} e B _{2 x 3}, então não existe o produto
• Se A _{4 x 2} e B _{2 x 1}, então ( A . B ) _{4 x 1}
  

Propriedades

Verificadas as condições de existência para a multiplicação de matrizes, valem as seguintes propriedades:

a) associativa: ( A . B) . C = A . ( B . C )

b) distributiva em relação à adição: A . ( B + C ) = A . B + A . C ou ( A + B ) . C = A . C + B . C

c) elemento neutro: A . I_n = I_n . A = A, sendo I_n a matriz identidade de ordem n

Vimos que a propriedade comutativa, geralmente, não vale para a multiplicação de matrizes. Não vale também o anulamento do produto, ou seja: sendo 0 _{m x n} uma matriz nula, A .B =0 _{m x n} não implica, necessariamente, que A = 0 _{m x n} ou B = 0 _{m x n}.

Matriz inversa

Dada uma matriz A, quadrada, de ordem n, se existir uma matriz A', de mesma ordem, tal que A . A' = A' . A = I_n , então A' é matriz inversa de A . representamos a matriz inversa por A^-1 .

www.somatematica.com.br