Área total do cone

Por Marcelo Rigonatto

Cone

O cone é um sólido geométrico classificado como corpo redondo por apresentar, assim como o cilindro, uma de suas faces arredondadas. Ele pode ser considerado um tipo especial de pirâmide, sendo que algumas de suas propriedades são semelhantes às das pirâmides. É possível notar a aplicação desse sólido em embalagens, sinalização de trânsito, formatos de produtos, casquinhas de sorvete e outros.

Nosso objeto de estudo é o cone circular reto, também chamado de cone de revolução por ser gerado pela rotação (revolução) de um triângulo retângulo em torno de um de seus catetos. Considere um cone circular reto de altura h, raio da base r e geratriz g, como mostra a figura.

Para determinar a área total de um cone é necessário realizar sua planificação.

Observe que sua superfície lateral é formada por um setor circular. Esse fato requer bastante atenção para o cálculo de sua área. É fácil notar que a área total do cone é obtida através da seguinte expressão:

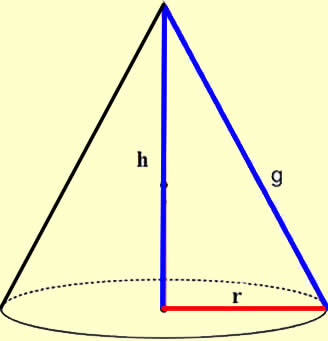
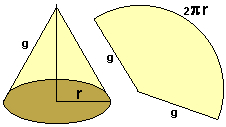
área total = área da base + área lateral

Como a base do cone é uma circunferência de raio r, sua área é dada por:

área da base = π∙r²

Já a superfície lateral pode ter sua área determinada através da seguinte sentença matemática:

área lateral= π∙r∙g

Dessa forma, podemos obter uma expressão para a área total do cone em função da medida do raio da base e do valor da geratriz.

S_t = π∙r² + π∙r∙g

Colocando πr em evidência, a fórmula pode ser reescrita da seguinte forma:

S_t = π∙r∙(g + r)

Onde
S_t → é a área total
r → é a medida do raio da base
g → é a medida da geratriz

Há uma relação importante entre a altura, a geratriz e o raio da base do cone:

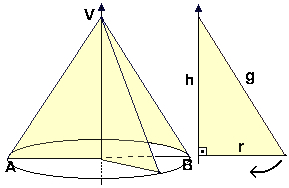
g² = h² + r²

Vejamos alguns exemplos de aplicação da fórmula da área total do cone.

Exemplo 1. Calcule a área total de um cone de 8 cm de altura, sabendo que o raio da base mede 6 cm. (Use π = 3,14)

Solução: Temos os dados do problema:

h = 8 cm
r = 6 cm
g = ?
S_t = ?

Observe que para determinar a área total é necessário conhecer a medida da geratriz do cone. Como sabemos a medida do raio e da altura, basta utilizar a relação fundamental envolvendo os três elementos:

g² = h² + r²
g² = 82 + 62
g² = 64 + 36
g² = 100
g = 10 cm

Conhecida a medida da geratriz, podemos calcular a área total.

S_t = π∙r∙(g + r)
S_t = 3,14 ∙ 6 ∙ (10 + 6)
S_t = 3,14 ∙ 6 ∙ 16
S_t = 301,44 cm²

Exemplo 2. Deseja-se construir um cone circular reto, utilizando para isso papel. Sabendo que o cone deve apresentar 20 cm de altura e que a geratriz terá 25 cm de comprimento, quantos centímetros quadrados de papel serão gastos para confeccionar esse cone?

Solução: Para resolver esse problema devemos obter o valor da área total do cone. Os dados foram:

h = 20 cm
g = 25 cm
r = ?
S_t = ?

É necessário conhecer a medida do raio da base para encontrar o total de papel gasto. Segue que:

g² = h² + r²
252 = 202 + r²
625 = 400 + r²
r² = 625 – 400
r² = 225
r = 15 cm

Conhecidas as medidas da altura, da geratriz e do raio, basta aplicar a fórmula da área total.

S_t = π∙r∙(g + r)
S_t = 3,14 ∙ 15 ∙ (25 + 15)
S_t = 3,14 ∙ 15 ∙ 40
S_t = 1884 cm²

Portanto, podemos afirmar que serão necessários 1884 cm² de papel para construir esse cone.

Exemplo 3. Determine a medida da geratriz de um cone circular reto que apresenta uma área total de 7536 cm² e raio da base medindo 30 cm.

Solução: Foram dados pelo problema:

S_t = 7536 cm²
r = 30 cm
g = ?

Segue que:

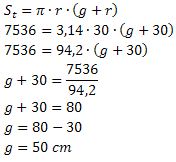
Portanto, a geratriz desse cone mede 50 cm de comprimento.