Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
No estudo da função do 2º grau percebemos que seu gráfico é uma parábola e que esse gráfico apresenta pontos notáveis e de bastante aplicação na vida cotidiana e no estudo de outras ciências. Esses pontos são: as raízes da função e o vértice da parábola. As raízes determinam quais os pontos onde o gráfico intercepta o eixo das abscissas (eixo x); o vértice pode ser o ponto de máximo absoluto ou de mínimo absoluto da função, ou seja, o maior ou o menor valor que a função pode assumir em todo o seu domínio.
Iremos fazer um estudo dos pontos de máximo e mínimo absolutos da função do 2º grau e compreender sua utilidade nos contextos mais diversos.
Considere uma função do 2º grau qualquer, do tipo f(x) = ax2 + bx + c, com a ≠ 0. Sabemos que seu gráfico é uma parábola e que a concavidade da parábola varia de acordo com o coeficiente a. Ou seja,
Se a < 0 → a concavidade da parábola é voltada para baixo;
Se a > 0 → a concavidade da parábola é voltada para cima;
Sabemos também que o valor de Δ = b2 – 4ac determina quantos pontos a parábola intercepta o eixo x. Ou seja,
Δ > 0 → a função tem duas raízes reais, logo intercepta o eixo x em dois pontos;
Δ < 0 → a função não possui raízes reais, logo não intercepta o eixo x;
Δ = 0 → a função possui apenas uma raiz real, logo intercepta o eixo x em apenas um ponto;
Vimos anteriormente que o vértice da parábola pode ser um ponto de mínimo absoluto ou de máximo absoluto, e o que determina um caso ou outro é a concavidade da parábola.
Se a concavidade for voltada para baixo, a função apresenta ponto de máximo absoluto.
Se a concavidade for voltada para cima, a função apresenta ponto de mínimo absoluto.
As coordenadas do vértice da parábola são dadas por:
Exemplo 1: Dadas as funções abaixo, determine se elas possuem ponto de máximo ou mínimo absoluto e as coordenadas desses pontos.
a) f(x) = 3x2 – 4x + 1
Solução: Observando a função, podemos afirmar que a = 3 > 0. Portanto, o gráfico da função é uma parábola com a concavidade voltada para cima. Isso implica que a função apresenta um ponto de mínimo absoluto. Vimos que esse ponto é o vértice da parábola e para determinar suas coordenadas utilizamos as fórmulas:
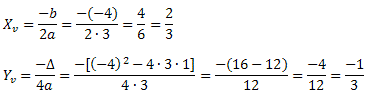
Dessa forma, o ponto de máximo absoluto, que é o vértice da parábola, tem coordenadas:
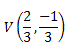
Exemplo 2. O lucro de uma fábrica na venda de determinado produto é dado pela função
L(x) = – 5x2 + 100x – 80, onde x representa o número de produtos vendidos e L(x) é o lucro em reais. Determine:
a) O lucro máximo obtido pela fábrica na venda desses produtos.
Solução: Como a função que determina o lucro da fábrica, L(x) = – 5x2 + 100x – 80, é uma função do 2º grau, percebemos que a = – 5 < 0. Isso implica que a parábola que representa essa função tem a concavidade voltada para baixo, tendo, portanto, um ponto de máximo absoluto, que é o vértice da parábola. O lucro máximo da empresa será dado pelo Yv (coordenada y do vértice). Assim, teremos:
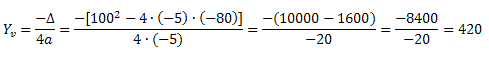
Portanto, o lucro máximo da fábrica será de R$ 420,00.
b) Quantos produtos precisam ser vendidos para obtenção do lucro máximo.
Solução: O número de produtos a serem vendidos para obtenção do lucro máximo será dado pelo Xv (coordenada x do vértice). Teremos:
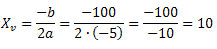
Concluímos que a fábrica precisa vender 10 produtos para obter o lucro máximo desejado.
Marcelo Rigonatto
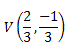
Exemplo 2. O lucro de uma fábrica na venda de determinado produto é dado pela função
L(x) = – 5x2 + 100x – 80, onde x representa o número de produtos vendidos e L(x) é o lucro em reais. Determine:
a) O lucro máximo obtido pela fábrica na venda desses produtos.
Solução: Como a função que determina o lucro da fábrica, L(x) = – 5x2 + 100x – 80, é uma função do 2º grau, percebemos que a = – 5 < 0. Isso implica que a parábola que representa essa função tem a concavidade voltada para baixo, tendo, portanto, um ponto de máximo absoluto, que é o vértice da parábola. O lucro máximo da empresa será dado pelo Yv (coordenada y do vértice). Assim, teremos:
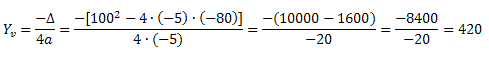
Portanto, o lucro máximo da fábrica será de R$ 420,00.
b) Quantos produtos precisam ser vendidos para obtenção do lucro máximo.
Solução: O número de produtos a serem vendidos para obtenção do lucro máximo será dado pelo Xv (coordenada x do vértice). Teremos:
Concluímos que a fábrica precisa vender 10 produtos para obter o lucro máximo desejado.
Nenhum comentário:
Postar um comentário