Colégio Estadual Dinah Gonçalves
Número Imaginário
Marcos Noé
Unidade imaginária
Ao resolvermos uma equação do 2º grau utilizando o método de Bháskara, respeitamos algumas condições de acordo com o valor do discriminante. Se ele for maior ou igual a zero, continuamos a resolver a equação. Caso seja menor que zero, isto é, um número negativo, dizemos que a equação não possui raízes reais, em virtude de o valor do discriminante pertencer a uma raiz. A afirmativa condiciona-se ao fato de que dentre o conjunto dos números reais, não existe raiz quadrada de números negativos. Observe a seguinte equação:
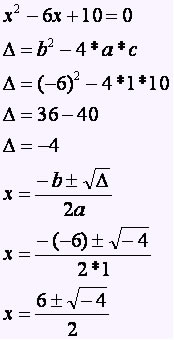
O valor do discriminante é igual a um número negativo (∆ = −4). Esse tipo de equação ficou por muito tempo sem resolução, pois enquadrava-se na situação da raiz quadrada de um número negativo. Somente após um longo período de pesquisas e estudos, matemáticos anunciaram a resolução com o auxílio de um número imaginário. O mesmo era representado pelo símbolo i² e associava seu valor a −1. Observe como representar a raiz negativa da equação anterior:

Dessa forma, as equações em que o valor do discriminante fosse um número negativo, seriam resolvidas aplicando as técnicas do número imaginário, obtendo assim, a raiz quadrada deste número negativo. Veja:
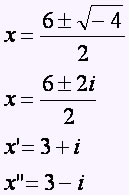
Com essa nova descoberta surgiu o conjunto dos números complexos, formados por uma parte real e outra parte imaginária. Por exemplo, as raízes da equação do 2º grau x² − 6x + 10 = 0, são x’ = 3 + i e x” = 3 − i. As raízes são números complexos onde a parte real de x’ é igual a 3 e a parte imaginária +i e a parte real de x” é 3 e a parte imaginária −i.
Exemplo
Vamos determinar as raízes da seguinte equação do 2º grau: −x² + 4x − 29 = 0.
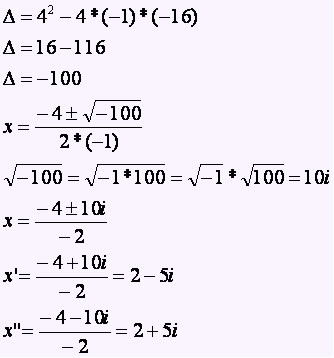
As raízes da equação −x² + 4x − 29 = 0 são:
x’ = 2 − 5i
x” = 2 + 5i
Nenhum comentário:
Postar um comentário