Representação Matricial de um Sistema

Um sistema de equações pode ser representado na forma de uma matriz. Os coeficientes das incógnitas serão os elementos da matriz que ocuparão as linhas e as colunas de acordo com o posicionamento dos termos no sistema. O sistema 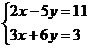terá a seguinte representação matricial: .


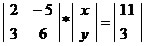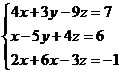
Observe mais alguns sistemas representados por matrizes.

Exemplo 1

Sistema de equações com três equações e três incógnitas: x, y e z.

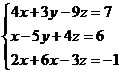
Representação matricial

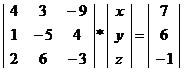
Exemplo 2
Sistema de equações

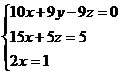
Representação matricial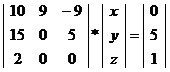


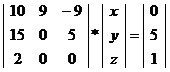
Essa relação entre sistemas de equações e matrizes fora estabelecida no intuito de determinar o valor das incógnitas através de técnicas envolvendo cálculo de determinantes de matrizes. Nesses casos, o método utilizado é a resolução de acordo com a Regra de Cramer, que consiste na relação entre a matriz dos coeficientes das incógnitas e a matriz dos coeficientes independentes, descartando a matriz das variáveis.

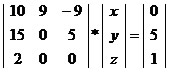
Matriz dos coeficientes

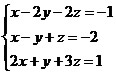
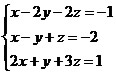
A regra de Cramer estabelece que, se D ≠ 0 temos:

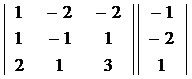
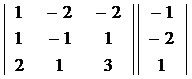
x = Dx/D
y = Dy/D
z = Dz/D
No caso desse sistema obtemos as seguintes matrizes:

Na matriz Dx, a coluna dos coeficientes de x foi substituída pelos coeficientes independentes.

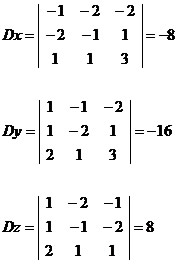
Na matriz Dy, a coluna dos coeficientes de y foi substituída pelos coeficientes independentes.

Na matriz Dz, a coluna dos coeficientes de z foi substituída pelos coeficientes independentes.
x = Dx/D → –8/–8 = 1
y = Dy/D → –16/–8 = 2
z = Dz/D → 8 / –8 = –1

A solução do sistema é x = 1, y = 2 e z = –1.
www.mundoeducacao.com.br