Teorema de Pitágoras
Marcos Noé
Teorema de Pitágoras
O Teorema de Pitágoras pode ser aplicado em qualquer triângulo retângulo no intuito de determinar uma das medidas quando conhecidas as outras duas. O Teorema não se restringiu somente ao triângulo retângulo, de acordo com estudos da época, eram conhecidos os números inteiros e as frações, sendo através das aplicações do Teorema iniciado o estudo dos números irracionais.
O Teorema consistia na seguinte relação:
“A medida do quadrado da hipotenusa é igual à soma das medidas dos quadrados dos catetos”

A relação dos números irracionais com o Teorema de Pitágoras consiste no cálculo da medida da diagonal do quadrado, observe:
Dado o quadrado ABCD com lados medindo 1 unidade, vamos determinar a sua diagonal. A diagonal divide o quadrado em dois triângulos retângulos, sendo assim, podemos notar que a diagonal do quadrado é a hipotenusa dos dois triângulos retângulos. Aplicando o Teorema de Pitágoras temos:
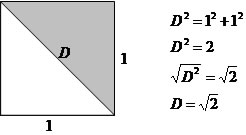
Veja que √2 não possui raiz exata, com o auxílio de uma calculadora chegaremos ao seguinte resultado 1,414213562... . Esse tipo de número não era conhecido, pois depois da vírgula não formava períodos como os racionais. Essa situação colocou em dúvida a descoberta de Pitágoras por algum tempo, pois não se tinha uma explicação definida para esse tipo de numeral, contrariando toda a teoria de representar um número através de uma relação (fração).
Com o passar dos séculos e a evolução da Matemática, os números irracionais foram aceitos e introduzidos nos conceitos matemáticos, tornando o Teorema de Pitágoras ferramenta imprescindível nos estudos relacionados à Geometria.
Exemplos
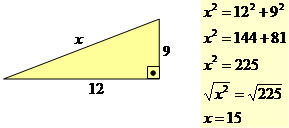
1 – Determine a medida da hipotenusa do triângulo representado pela figura a seguir:
Com o passar dos séculos e a evolução da Matemática, os números irracionais foram aceitos e introduzidos nos conceitos matemáticos, tornando o Teorema de Pitágoras ferramenta imprescindível nos estudos relacionados à Geometria.
Exemplos
1 – Determine a medida da hipotenusa do triângulo representado pela figura a seguir:

2 – Dado o triângulo retângulo a seguir, determine a medida do cateto y.
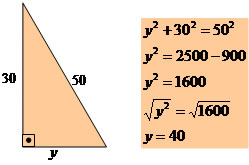
Nenhum comentário:
Postar um comentário