Triângulo equilátero inscrito numa circunferência

Professor de Matemática Antonio Carlos Carneiro Barroso

Colégio Estadual Dinah Gonçalves

email accbarroso@hotmail.com

Blog HTTP://ensinodematemtica.blogspot.com

http://accbarrosogestar.blogspot.com.br 

O uso da geometria plana, das suas definições, conceitos e fórmulas é muito comum em diversas situações cotidianas. Diariamente nos envolvemos com situações em que a geometria se faz presente, como o cálculo de comprimentos, áreas, medidas de ângulos e outras. É um dos ramos da matemática que mais apresenta aplicações na vida prática, portanto, fundamental é conhecer, compreender e aplicar suas fórmulas na resolução de situações-problema.

Vejamos como podemos determinar a área de um triângulo equilátero inscrito numa circunferência de raio r em função da medida do raio.

Considere um triângulo equilátero de lado l, inscrito numa circunferência de raio r, como mostra a figura.

Onde a é o apótema do triângulo equilátero.

O centro C da circunferência é o ortocentro e baricentro do triângulo equilátero. Logo, seu comprimento equivale a 1/3 do valor da altura do triângulo. Ou seja,

Dessa forma, podemos constatar, também, que o raio r equivale a 2/3 do valor da altura do triângulo. Assim, podemos escrever:

Verificamos também que o apótema equivale à metade do valor do raio da circunferência. Ou seja:

Sabemos que a área de qualquer triângulo é dada por:

A = base x altura

Para o triângulo equilátero, sabemos que:

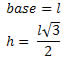
Logo, a área do triângulo equilátero será:

Nosso objetivo é determinar a área do triângulo equilátero em função do raio da circunferência. Temos que:

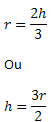
Daí, obtemos a seguinte igualdade:

Dessa forma, a área do triângulo equilátero inscrito numa circunferência, em função do raio r, será:

Vejamos alguns exemplos de aplicação.

Exemplo 1. Determine a área de um triângulo equilátero inscrito numa circunferência de 8 cm de raio.

Solução: Pelo enunciado, temos que r = 8 cm. A área do triângulo equilátero inscrito numa circunferência pode ser obtida conhecendo-se somente o valor do raio. Segue que:

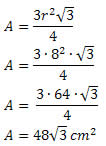
Exemplo 2. Um triângulo equilátero com lados medindo 10 cm está inscrito numa circunferência de raio r. Calcule a área dessa circunferência.

Solução: Para determinar a área da circunferência precisamos conhecer a medida de seu raio. Como sabemos a medida do lado do triângulo equilátero, podemos obter o valor de r pela fórmula:

Por Marcelo Rigonatto
Especialista em Estatística e Modelagem Matemática