A equação reduzida da circunferência é
dada pela expressão (x – a)² + (y – b)² = R². Para definir essa
expressão vamos analisar a situação da ilustração a seguir:
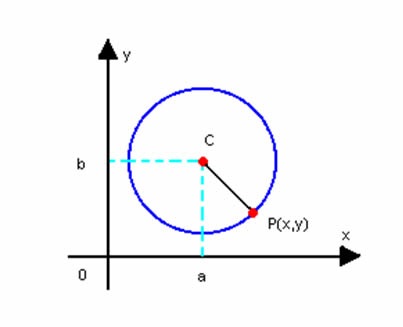
Na ilustração, a circunferência possui
centro C com coordenadas (a, b). O ponto genérico P possui as
coordenadas (x, y). Vamos estabelecer a distância entre os pontos C e P
utilizando a expressão matemática 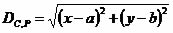 , de acordo com as definições da Geometria Analítica.
, de acordo com as definições da Geometria Analítica.
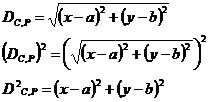
De acordo com a ilustração gráfica, a
distância entre os pontos C e P é considerado o raio da circunferência.
Dessa forma, substituiremos D²C,P por R (raio), observe:
(x – a)² + (y – b)² = R²
Vamos determinar a equação reduzida da circunferência com centro C (2, –9) e raio 6.
(x – a)² + (y – b)² = R²
(x – 2)² + (y + 9)² = 6²
(x – 2)² + (y + 9)² = 36
(x – 2)² + (y + 9)² = 6²
(x – 2)² + (y + 9)² = 36
(FEI–SP) Determine a equação da circunferência com centro no ponto C (2, 1) e que passa pelo ponto A (1, 1).
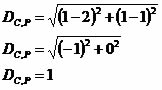
A distância entre o centro C e o ponto P corresponde à medida do raio.
(x – a)² + (y – b)² = R²
(x – 2)² + (y – 1)² = 1²
(x – 2)² + (y – 1)² = 1
A equação da circunferência com centro C
(2, 1) e que passa pelo ponto A (1, 1) possui como equação reduzida a
expressão matemática (x – 2)² + (y – 1)² = 1. A equação geral surgirá do
desenvolvimento da expressão reduzida (x – 2)² + (y – 1)² = 1, veja:
(x – 2)² + (y – 1)² = 1
x² – 4x + 4 + y² – 2y + 1 – 1 = 0
x² + y² – 4x – 2y + 4 = 0
Marcos Noé
x² – 4x + 4 + y² – 2y + 1 – 1 = 0
x² + y² – 4x – 2y + 4 = 0
Nenhum comentário:
Postar um comentário