Aplicação
Verifique a posição relativa entre as circunferências:
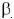 = x2 + y2 = 4 e = (x - 2)2 + y2 = 16.
= x2 + y2 = 4 e = (x - 2)2 + y2 = 16.
Solução:
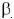 →C1 (0,0) e R1 = 2 C2 (2,0) e R2 = 4
→C1 (0,0) e R1 = 2 C2 (2,0) e R2 = 4
A distância entre seus centros é:
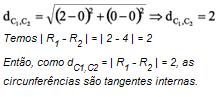
CÔNICAS OU LUGARES GEOMÉTRICOS
Denominamos lugar geométrico a um conjunto de pontos tais que todos eles (e só eles) possuem uma dada propriedade. A equação de um lugar geométrico do plano cartesiano é uma equação nas incógnitas x e y cujas soluções são os pares de coordenadas (x, y) dos pontos do lugar geométrico. Para obter tal equação, consideramos um ponto P (x, y) genérico e aplicamos a P a propriedade característica dos pontos do lugar geométrico. Neste número do Aprovar, estudaremos apenas a elipse e a hipérbole.
ELIPSE
É o lugar geométrico dos pontos de um plano tal que a soma de suas distâncias a dois pontos fixos, denominados focos, F1 e F2, é constante, igual a 2a e maior que a distância entre os focos (2a > 2c)
EQUAÇÃO DA ELIPSE COM CENTRO NA ORIGEM
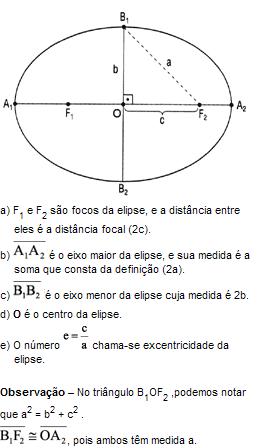
Considere a elipse com as extremidades do eixo maior nos pontos A1(-a, 0) e A2(a, 0), do eixo menor em B1(0, b) e B2(0, -b) e, conseqüentemente, o centro em O (0, 0). Considere também um ponto P (x, y) qualquer da curva. Com isso, obteremos, depois de certos procedimentos matemáticos, a equação reduzida da elipse.
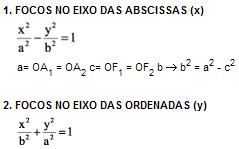
HIPÉRBOLE
É lugar geométrico dos pontos P (x, y) de um plano tal que a diferença (em módulo) de suas distâncias a dois pontos fixos F1 e F2 é constante (2a < alt="" src="http://www.iped.com.br/sie/uploads/8309.jpg" border="0" height="32" width="56">= 2c.
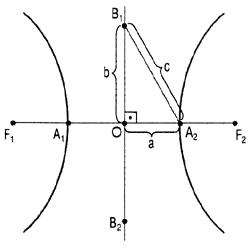
Na figura, temos:
a) F1 e F2 são os focos da hipérbole, sendo =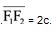 a distância focal.
a distância focal.
b) A1 e A2 são os vértices da hipérbole, sendo A1A2 = A1F2 - A1F1 = 2a (constante da definição) →eixo real.

EQUAÇÃO DA HIPÉRBOLE COM CENTRO NA ORIGEM
Considere uma hipérbole na qual os focos pertencem ou ao eixo das abscissas ou ao eixo das ordenadas, e o centro é a origem O (0, 0). Considere também um ponto P (x, y) qualquer da curva. Com esses dados, obteremos, depois de alguns procedimentos matemáticos, a equação reduzida da hipérbole.

Aplicações
01. Obter a equação da elipse de focos F1(-2,0) e F2(2,0), sabendo ainda que seu semi-eixo menor é b = 3.
Solução:
De início, note que os focos pertencem ao eixo Ox (isto é, o eixo maior é horizontal) e que a semidistância focal é igual a 2. Então:

02. Determinar a equação da hipérbole de focos F1(-3,0) e F2(3,0) cujo semi-eixo real é a = 2.
Solução
Das: coordenadas dos focos concluiu-se que a hipérbole tem seu eixo real situado no eixo Ox e que a semi distância focal é c = 3. Assim,
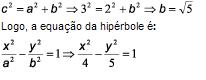
www.colegioweb.com.br
Verifique a posição relativa entre as circunferências:
Solução:
A distância entre seus centros é:
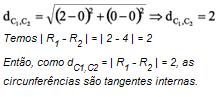
CÔNICAS OU LUGARES GEOMÉTRICOS
Denominamos lugar geométrico a um conjunto de pontos tais que todos eles (e só eles) possuem uma dada propriedade. A equação de um lugar geométrico do plano cartesiano é uma equação nas incógnitas x e y cujas soluções são os pares de coordenadas (x, y) dos pontos do lugar geométrico. Para obter tal equação, consideramos um ponto P (x, y) genérico e aplicamos a P a propriedade característica dos pontos do lugar geométrico. Neste número do Aprovar, estudaremos apenas a elipse e a hipérbole.
ELIPSE
É o lugar geométrico dos pontos de um plano tal que a soma de suas distâncias a dois pontos fixos, denominados focos, F1 e F2, é constante, igual a 2a e maior que a distância entre os focos (2a > 2c)

EQUAÇÃO DA ELIPSE COM CENTRO NA ORIGEM
Considere a elipse com as extremidades do eixo maior nos pontos A1(-a, 0) e A2(a, 0), do eixo menor em B1(0, b) e B2(0, -b) e, conseqüentemente, o centro em O (0, 0). Considere também um ponto P (x, y) qualquer da curva. Com isso, obteremos, depois de certos procedimentos matemáticos, a equação reduzida da elipse.
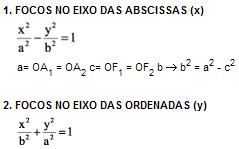
HIPÉRBOLE
É lugar geométrico dos pontos P (x, y) de um plano tal que a diferença (em módulo) de suas distâncias a dois pontos fixos F1 e F2 é constante (2a < alt="" src="http://www.iped.com.br/sie/uploads/8309.jpg" border="0" height="32" width="56">= 2c.

Na figura, temos:
a) F1 e F2 são os focos da hipérbole, sendo =
b) A1 e A2 são os vértices da hipérbole, sendo A1A2 = A1F2 - A1F1 = 2a (constante da definição) →eixo real.

EQUAÇÃO DA HIPÉRBOLE COM CENTRO NA ORIGEM
Considere uma hipérbole na qual os focos pertencem ou ao eixo das abscissas ou ao eixo das ordenadas, e o centro é a origem O (0, 0). Considere também um ponto P (x, y) qualquer da curva. Com esses dados, obteremos, depois de alguns procedimentos matemáticos, a equação reduzida da hipérbole.

Aplicações
01. Obter a equação da elipse de focos F1(-2,0) e F2(2,0), sabendo ainda que seu semi-eixo menor é b = 3.
Solução:
De início, note que os focos pertencem ao eixo Ox (isto é, o eixo maior é horizontal) e que a semidistância focal é igual a 2. Então:

02. Determinar a equação da hipérbole de focos F1(-3,0) e F2(3,0) cujo semi-eixo real é a = 2.
Solução
Das: coordenadas dos focos concluiu-se que a hipérbole tem seu eixo real situado no eixo Ox e que a semi distância focal é c = 3. Assim,
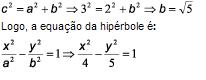
www.colegioweb.com.br
gostei da explicação muito bem elaborada
ResponderExcluirNa questão 1, o b^2 colocado na equação geral nao seria 9?!
ResponderExcluirNa questão 1, o b^2 colocado na equação geral nao seria 9?!
ResponderExcluir