São relações estabelecidas entre coeficientes e raízes da equação P(x) = 0. Se a equação do 2° grau ax² + bx + c = 0 tem raízes x1 e x2, então:
Dada a equação de grau 3 ax³ + bx² + cx + d = 0, de raízes x1, x2 e x3, pelo teorema da decomposição, temos:
Então:
Generalizando, para uma equação polinomial de grau n > 3, da forma:
Temos:
____________________________________________________________________________________________
____________________________________________________________________________________________
Exercícios:
1- Dada a equação x³ - 3x² + 5x – 8 = 0, de raízes x1, x2 e x3, determinar:
a) x1 + x2 + x3
b) x1x2 + x1x3 + x2x3
c) x1x2x3
2- Resolver a equação x³ - 9x² + 26x – 24 = 0, sabendo que suas raízes estão em PA (Progressão Aritmética).
3- Resolver a equação x³ - 14x² + 56x – 64 = 0, sabendo que suas raízes estão em PG (Progressão Geométrica).
fazendomatematica.com
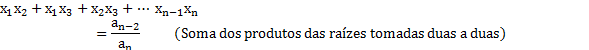
Nenhum comentário:
Postar um comentário