Cálculo do cofator de uma matriz quadrada

Marcelo Rigonatto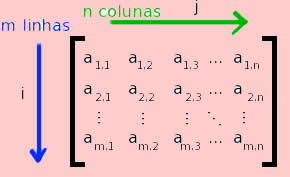

Matriz

O cálculo do determinante de uma matriz quadrada, muitas vezes, pode ser simplificado utilizando algumas propriedades e teoremas. O cofator é um elemento que facilitará esses cálculos quando aplicado ao Teorema de Laplace. Vamos definir o que é o cofator.

Considere uma matriz quadrada M de ordem n ≥ 2 e seja a_ij um elemento de M. Denomina-se cofator de a_ij o número A_ij tal que A_ij = (-1)^(i+j)∙D_ij. Onde D_ij é o determinante da matriz obtida de M após ter eliminado sua i-ésima linha e j-ésima coluna.
Lendo a definição parece se tratar de um cálculo complexo, mas é muito simples. Vejamos alguns exemplos para melhor compreender a definição e como realizar o cálculo do cofator.

Exemplo 1. Dada a matriz M abaixo, qual é o cofator do elemento a₂₃?

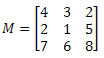
Solução: Queremos determinar o cofator do elemento a₂₃. Dessa forma, temos que i = 2 e j = 3. Teremos, então, que eliminar a 2ª linha e a 3ª coluna de M:

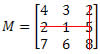
Assim, obtemos:

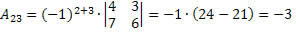
Portanto, o cofator do elemento a₂₃ é A₂₃ = – 3.

Exemplo 2. Calcule o cofator do elemento a₄₁ da matriz A abaixo.

Solução: Queremos determinar o cofator do elemento a₄₁. Assim, temos que i = 4 e j = 1. Teremos que eliminar a 4ª linha e a 1ª coluna de A:

Segue que:

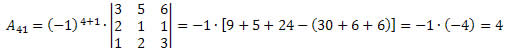
Portanto, o cofator do elemento a₄₁ é A₄₁ = – 4.

Exemplo 3. Qual o cofator do elemento a₂₂ da matriz G abaixo?

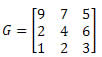
Solução: Como queremos determinar o cofator do elemento a₂₂, temos que i = 2 e j = 2. Dessa forma, teremos que eliminar a 2ª linha e a 2ª coluna da matriz G:

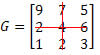
Segue que:

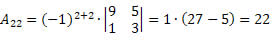
Portanto, o cofator do elemento a₂₂ é A₂₂ = 22.