Professor de Matemática no Colégio Estadual Dinah Gonçalves
E Biologia na rede privada de Salvador-Bahia
Professor Antonio Carlos carneiro Barroso
email accbarroso@hotmail.com
Extraído de http://www.alunosonline.com.br
Arranjos Simples
Arranjo
Diferentes pela natureza: (1,2) e (2,3)
Pela ordem dos elementos: (1,3) e (3,1), (1,2) e (2,1)
Nesse caso, o número de arranjos é indicado por A3,2. Os arranjos podem ser calculados utilizando dois métodos, o princípio fundamental da contagem ou pela expressão:
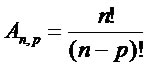
Exemplo 1
Um campeonato de futsal será decidido em um quadrangular final envolvendo as seguintes seleções: Brasil, Itália, Espanha e Argentina. De quantas maneiras distintas o pódio poderá ser formado.
O pódio deverá contar com três seleções, 1º, 2º e 3º lugares. De modo que:
4 seleções disputam o 1º lugar.
3 seleções disputam o 2º lugar.
2 seleções disputam o 3º lugar .
Utilizando a fórmula de Arranjos
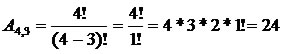
Utilizando o PFC
A4,3 = 4! = 4*3*2*1 = 24
O pódio deverá ser formado por 24 maneiras distintas.
Exemplo 2
Para ocupar os cargos de presidente e vice-presidente da Câmara Federal, candidataram-se dez deputados federais. De quantas maneiras distintas a escolha poderá ser feita?
Temos dez candidatos para ocuparem duas vagas, dessa forma, temos o seguinte arranjo A10,2.
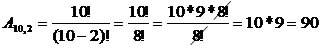
A4,3 = 4! = 4*3*2*1 = 24
O pódio deverá ser formado por 24 maneiras distintas.
Exemplo 2
Para ocupar os cargos de presidente e vice-presidente da Câmara Federal, candidataram-se dez deputados federais. De quantas maneiras distintas a escolha poderá ser feita?
Temos dez candidatos para ocuparem duas vagas, dessa forma, temos o seguinte arranjo A10,2.
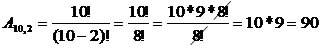
A escolha pode ser feita de 90 maneiras distintas.
Nenhum comentário:
Postar um comentário