Bháskara : Resolvendo uma Equação Completa do 2º Grau

Marcos Noé

Fórmula de Bháskara

Equações do tipo ax + b = 0, com a e b números reais e a ≠ 0, são consideradas do 1º grau e possuem uma única raiz real. Já as equações completas do 2º grau possuem a seguinte lei de formação ax² + bx + c = 0, com a, b e c números reais e a ≠ 0 e devem ser resolvidas com o uso da fórmula de Bháskara:



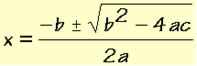
onde a, b e c são os coeficientes da equação.

Discriminante: ∆ = b² - 4ac
Condições:
∆> 0 (número positivo): duas raízes reais e diferentes
∆< 0 (número negativo): nenhuma raiz real
∆= 0: duas raízes reais

Exemplo 1
Quais os coeficientes da equação 2x² + 5x – 6 = 0?
a = 2 b = 5 c = – 6

Exemplo 2
Calcule as raízes, se existirem, da seguinte equação do 2º grau: x² + 4x – 5 = 0.
Temos que: a = 1 b = 4 c = -5



Nem sempre o valor do discriminante será um número quadrado perfeito, acompanhe o exemplo 3:
x² - 3x + 1 = 0