Lei dos cossenos
Marcelo Rigonatto
Triângulo
Vejamos a demonstração da lei dos cossenos:
Considere o triângulo acutângulo abaixo, sendo CH a altura relativa ao lado AB.
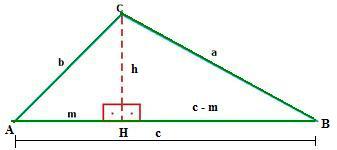
No triângulo BCH, temos que:
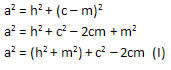
No triângulo ACH, temos que:
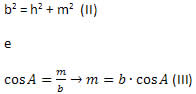
Substituindo (II) e (III) em (I), obtemos:
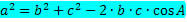
De forma análoga, obtemos:

As três igualdades anteriores são chamadas de Lei dos Cossenos, que diz: “Num triângulo qualquer, o quadrado de um lado é igual à soma dos quadrados dos outros dois lados menos o dobro do produto desses lados pelo cosseno do ângulo por eles formado”.
Lembre-se que a Lei dos cossenos vale para qualquer triângulo.
Vejamos alguns exemplos de aplicação.
Exemplo 1. Determine o valor de x no triângulo ABC acutângulo abaixo.
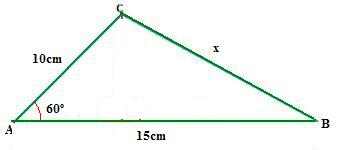
Solução: Aplicando a lei dos cossenos, temos que:
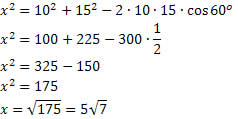
Exemplo 2. Determine o valor de y no triângulo obtusângulo abaixo.
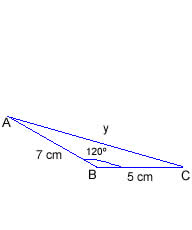
Solução: Lembrando que a lei dos cossenos também é válida para o triângulo obtusângulo, temos que:
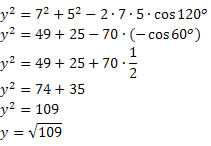
Nenhum comentário:
Postar um comentário