Algumas regiões planas se assemelham a polígonos conhecidos como triângulo, quadrado, retângulo, losango, paralelogramo, trapézio, pentágono, hexágono, entre outros, onde cada um possui uma fórmula específica para determinar a área de sua superfície. Mas algumas regiões possuem formatos não definidos pela Matemática, são as formas irregulares. Nesse caso, precisamos tentar decompor a figura em partes conhecidas, calculando individualmente a área de cada uma, as quais serão somadas constituindo a área total da região. Observe a área de uma região irregular:
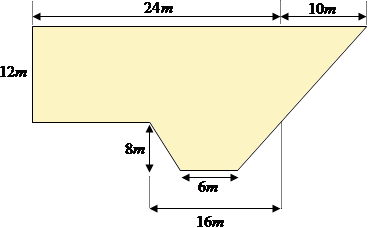
Decomposição da área em figuras conhecidas:
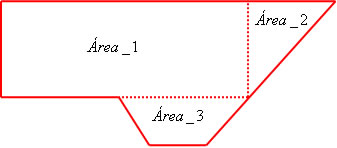
A área da região é constituída de um retângulo, um triângulo e um trapézio. Agora basta determinarmos as áreas de cada figura.
Área 1 – Retângulo
O retângulo referente a área 1 possui as seguintes dimensões:

Sua área é calculada multiplicando o comprimento pela largura:
A = 24 * 12
A = 288 m²
Área 2 – Triângulo
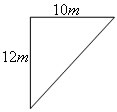
A área de uma região triangular é calculada através da metade da multiplicação da base pela altura.
A = (10*12) / 2
A = 120 / 2
A = 60 m²
Área 3 – Trapézio
A = (10*12) / 2
A = 120 / 2
A = 60 m²
Área 3 – Trapézio
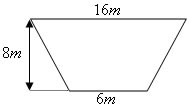
A área de um trapézio é dada pela seguinte expressão: 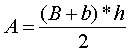 , onde:
, onde:
B: base maior
b: base menor
h: altura
Então:
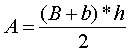 , onde:
, onde:B: base maior
b: base menor
h: altura
Então:
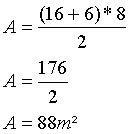
A área total da região é dada pelo somatório das áreas das regiões 1, 2 e 3:
Área total = 288m² + 60m² + 88m²
Área total = 436 m²
Qualquer região irregular pode ser decomposta em figuras mais simples, porém, em algumas situações, o cálculo pode ficar um pouco mais complexo. Para tais situações, a área da região é determinada através de integrais (conteúdo relacionado ao ensino superior).
Graduado em Matemática
Ótima postagem, bastante interessante para rever ou aprender. O processo é bastante calmo ( pelo menos nesse exemplo) kkkk
ResponderExcluirodiarioeducacional.blogspot.com