Definimos como círculo a região limitada por uma circunferência de raio r e de diâmetro 2r.
Elementos de um círculo ou circunferência
Dada uma região circular, podemos ter: raio, diâmetro, corda, centro, arcos. Veja a figura:
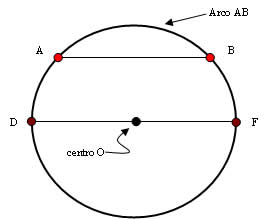
segmento de reta AB: corda (segmento que parte de um ponto ao outro da circunferência)
segmento de reta DF: diâmetro (corda que passa pelo centro do círculo)
segmento de reta OF e OD: raio (segmento de reta que liga o centro a um ponto da circunferência)
Ângulo central de um círculo
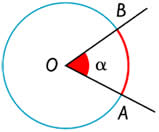
É o ângulo que tem o seu vértice localizado no centro da região circular. Observe na figura que AÔB é um ângulo central, sendo o arco AB correspondente ao ângulo.
Ângulo inscrito
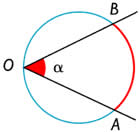
O ângulo é inscrito quando o seu vértice está localizado em qualquer ponto da circunferência e seus lados sejam considerados cordas da circunferência.
Elementos de um círculo ou circunferência
Dada uma região circular, podemos ter: raio, diâmetro, corda, centro, arcos. Veja a figura:

segmento de reta AB: corda (segmento que parte de um ponto ao outro da circunferência)
segmento de reta DF: diâmetro (corda que passa pelo centro do círculo)
segmento de reta OF e OD: raio (segmento de reta que liga o centro a um ponto da circunferência)
Ângulo central de um círculo
É o ângulo que tem o seu vértice localizado no centro da região circular. Observe na figura que AÔB é um ângulo central, sendo o arco AB correspondente ao ângulo.

Ângulo inscrito
O ângulo é inscrito quando o seu vértice está localizado em qualquer ponto da circunferência e seus lados sejam considerados cordas da circunferência.

Relação entre ângulo central e ângulo inscrito
Ao analisarmos uma circunferência e constatarmos que o ângulo central e o ângulo inscrito possuem o mesmo arco, podemos dizer que o valor do ângulo central é o dobro do valor do ângulo inscrito.
Exemplo
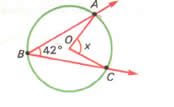
1 – Qual o valor do ângulo central indicado por x na figura:
x = 2*42º
x = 84º
Nenhum comentário:
Postar um comentário