A racionalização de denominadores consiste em se obter uma fração equivalente com denominador racional, para substituir uma outra com denominador irracional.
Conseguimos isto realizando algumas operações que eliminam o radical do denominador.
Iremos analisar três casos em particular.
Quando o Denominador é uma Raiz Quadrada
Este é o caso mais simples, quando tratamos radicais com índice igual a dois.
Vamos analisar a seguinte fração:
É sabido que podemos eliminar o radical se multiplicarmos  por ele mesmo. Vejamos:
por ele mesmo. Vejamos:
Partimos de  e chegamos a 5.
e chegamos a 5.
A conversão foi realizada em bem mais passos que o necessário, apenas para que você se recorde das principais propriedades da radiciação, que torna a conversão possível.
Então quando temos um radical de índice dois, podemos eliminá-lo multiplicando-o por ele mesmo, pois 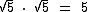 e além disto, para que nova a fração seja equivalente à fração original, também precisamos multiplicar o numerador pelo mesmo valor:
e além disto, para que nova a fração seja equivalente à fração original, também precisamos multiplicar o numerador pelo mesmo valor:
Neste nosso exemplo  é o fator racionalizante da fração, pois a racionalizamos multiplicando ambos os seus termos por tal fator.
é o fator racionalizante da fração, pois a racionalizamos multiplicando ambos os seus termos por tal fator.
Genericamente o fator racionalizante de um denominador  é o próprio
é o próprio 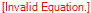 .
.
Exemplos



Quando o Denominador é uma Raiz Não Quadrada
Agora vamos tratar um caso cujo índice seja diferente de dois, ou seja, um caso onde não temos uma raiz quadrada.
Observe a fração a seguir:
Neste caso de nada adianta multiplicarmos o radical por ele mesmo, pois não conseguiremos eliminá-lo. Veja o que acontece quando o fazemos:
Perceba que no caso anterior havíamos partido de  e passamos por 51, o que nos permitiu chegarmos a 5.
e passamos por 51, o que nos permitiu chegarmos a 5.
Note que neste caso, porém, partindo-se de  chegamos a
chegamos a 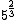 e como 2 não é divisível por 3, não conseguimos eliminar o radical.
e como 2 não é divisível por 3, não conseguimos eliminar o radical.
Então o que precisamos fazer?
Obviamente devemos multiplicar o radical, por um outro fator de sorte que consigamos chegar a 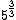 e não a
e não a 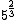 .
.
Qual fator é este?
É muito simples. Veja o ponto chave abaixo:
Qual é o número que somado a 1 dá 3?
É dois, pois 3 - 1 = 2.
Então o fator racionalizante da fração é 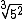 , pois:
, pois:
Logo:
Podemos então concluir que o fator racionalizante de um denominador 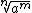 é igual a
é igual a  .
.
Exemplos



Quando o Denominador é uma Soma ou Diferença de Dois Quadrados
Agora no último caso a ser tratado, veremos como devemos proceder quando no denominador da fração temos uma soma ou diferença de um ou dois radicais com índice igual a 2.
Vejamos a fração abaixo:
Como pode observar, os métodos analisados acima não nos permitem racionalizar este tipo de fração. Para fazê-lo precisamos recorrer a um produto notável, mais especificamente ao produto da soma pela diferença de dois termos.
Mais especificamente, neste produto notável, o produto da soma pela diferença de dois termos é igual ao quadrado do primeiro termo, menos o quadrado do segundo termo. Algebricamente temos:
Conseguiu perceber como podemos utilizar este conceito para racionalizarmos a fração proposta?
Parabéns se conseguiu, mas se não conseguiu tudo, daqui a pouco você estará apto a fazê-lo.
Vamos ver o que acontece quando substituímos a por  e b por
e b por 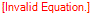 :
:
Percebeu agora?
Observe que originalmente tínhamos a expressão 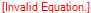 que multiplicamos por
que multiplicamos por 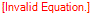 , perceba que invertemos o sinal, trocamos "+" por "-", se tivéssemos "-", o teríamos trocado por "+".
, perceba que invertemos o sinal, trocamos "+" por "-", se tivéssemos "-", o teríamos trocado por "+".
Como elevamos 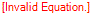 e
e 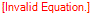 ao quadrado, eliminamos assim os radicais.
ao quadrado, eliminamos assim os radicais.
Como nos casos anteriores, devemos multiplicar ambos os termos da fração pelo fator racionalizante, que neste exemplo é 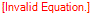 :
:
Neste último caso o fator racionalizante de um denominador 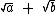 será
será 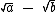 e vice-versa.
e vice-versa.
Exemplos



Neste último exemplo convertemos tanto 18 em 2 . 32, quanto 12 em 22 . 3 através da decomposição em fatores primos, que você pode revisar se for o caso. Nós também disponibilizamos no site uma calculadora para a fatoração de números naturais, que pode lhe ajudar muito a entender melhor como funciona o método de decomposição de um número natural em seus fatores primos.
www.matematicadidatica.com.br
Nenhum comentário:
Postar um comentário