Algumas integrais, cujo integrando consiste numa fração racional, ou seja, uma função do tipo:
onde p(x) e q(x) são polinômios reais com q ≠
0, são facilmente integráveis por substituição ou por partes, ou mesmo
diretamente. Mas isso nem sempre ocorre e o integrando pode não ser
facilmente calculada ou mesmo impossível por estes métodos. Neste caso,
podemos decompor a fração que define o integrando em frações parciais.
O
método consiste em reescrever a fração do integrando numa soma de
outras frações mais simples, de modo que a integração seja
necessariamente mais simples. A decomposição é feita a partir de
fatoração do polinômio q(x) que aparece no denominador, associando a cada fator linear ou quadrático irredutível uma ou mais frações parciais.
Um polinômio em x é uma função da forma:
onde os coeficientes são constantes, a0 ≠ 0 e n é um inteiro positivo que também pode ser nulo.
Sendo
assim, se dois polinômios do mesmo grau são iguais, qualquer que seja o
valor atribuído à variável nos dois polinômios são iguais.
Todo
polinômio de coeficientes reais pode ser expresso, pelo menos
teoricamente, como um produto de fatores lineares reais, da forma ax + b e fatores de segundo grau, irredutíveis, da forma ax2 + bx + c.
Uma função:
onde f (x) e g (x) são polinômios, é chamada de fração racional.
Se o grau de f (x) for menor que o grau de g (x), F (x) é uma fração racional própria; caso contrário, F (x) é denominada imprópria.
Uma fração racional imprópria pode ser expressa como a soma de um polinômio e de uma fração racional própria. Assim:
Toda
fração racional própria pode ser expressa, pelo menos teoricamente,
como uma soma de frações mais simples: frações parciais, cujos
denominadores são da forma:
onde n
é um inteiro positivo. Podemos ter quaro casos distintos, dependendo de
como os denominadores se apresentam. Vejamos cada caso individualmente.
Caso 1 – Fatores Lineares Distintos
A cada fator linear da forma ax + b que aparece uma vez no denominador de uma fração racional própria, corresponde a uma fração parcial da forma:
onde A é uma constante a determinar.
Exemplo 1: Achar a integral:
a) Primeiramente, fatoramos o denominador:
Fazemos:
Temos então que:
ou
b) Agora, vamos determinar as constantes. Para isso, dispomos de dois métodos:
Método Geral: Observando em (3) os coeficientes das potências semelhantes de x em ambos os membros da igualdade, podemos montar um sistema de equações:
Resolvendo o sistema, obtemos: A1 = 1/4 e A2 = –1/4.
Método Abreviado: Na igualdade (1), vamos observar os denominadores das frações parciais, que aparecem no segundo membro. Os valores para x que anulam os denominadores dessas frações são x = 2 e x = –2. Assim, substituímos estes valores em (2), obtendo:
Vejam que são os mesmos valores encontrados no método geral.
c) Agora, vamos reescrever a integral como:
E pelas propriedades dos logaritmos, temos:
Exemplo 2: Achar a integral:
a) Primeiramente, fatoramos o denominador:
Fazemos:
Temos então que:
ou
b) Agora, vamos determinar as constantes. Para isso, dispomos de dois métodos:
Método Geral: Observando em (3) os coeficientes das potências semelhantes de x em ambos os membros da igualdade, podemos montar um sistema de equações:
Resolvendo o sistema, obtemos: A1 = –1/6 , A2 = 3/10 e A3 = –2/15.
Método Abreviado: Na igualdade (1), vamos observar os denominadores das frações parciais, que aparecem no segundo membro. Os valores para x que anulam os denominadores dessas frações são x = 0, x = 2 e x = –3. Assim, substituímos estes valores em (2), obtendo:
Vejam que são os mesmos valores encontrados no método geral.
c) Agora, vamos reescrever a integral como:
E pelas propriedades dos logaritmos, temos:
Caso 2 – Fatores Lineares Repetidos
A cada fator linear da forma ax + b que aparece n vezes no denominador de uma fração racional própria, corresponde a uma soma de n frações parciais da forma:
onde A1, A2, ..., An são constantes a determinar.
Exemplo 3: Achar a integral:
a) Primeiramente, fatoramos o denominador:
Vejam que o fator que se repete é o (x – 1), pois (x – 1)2 = (x – 1)(x – 1). Como aparece duas vezes, fazemos
Temos então que:
ou
b) Agora, vamos determinar as constantes. Para isso, dispomos de dois métodos:
Método Geral: Observando em (3) os coeficientes das potências semelhantes de x em ambos os membros da igualdade, podemos montar um sistema de equações:
Resolvendo o sistema, obtemos: A1 = 1/2 , A2 = –1/2 e A3 = 4.
Método Abreviado: Na igualdade (1), vamos observar os denominadores das frações parciais, que aparecem no segundo membro. Os valores para x que anulam os denominadores dessas frações são x = –1 e x = 1. Assim, substituímos estes valores em (2), obtendo:
Ainda falta determinar a constante A2. Para isso, atribuímos qualquer valor para x e substituímos os valores já determinados para A1 e A2. Vamos supor x = 0:
Vejam que são os mesmos valores encontrados no método geral.
c) Agora, vamos reescrever a integral como:
E pelas propriedades dos logaritmos:
Exemplo 4: Achar a integral:
Veja que neste caso, o integrante é uma fração em que o numerador tem grau maior do que o denominador. Fazemos a divisão:
Fazemos:
Temos então que:
Método Abreviado: Na igualdade (1), vamos observar os denominadores das frações parciais, que aparecem no segundo membro. Os valores para x que anulam os denominadores dessas frações são x = 0, x = 1 e x = –2. Assim, substituímos estes valores em (2), obtendo:
c) Agora, vamos reescrever a integral como:
E pelas propriedades dos logaritmos:
Problemas para resolver em casa:
Referências:
[1] Cálculo Diferencial e Integral – Frank Ayres Jr – Coleção Schaum
[2] Cálculo II – Abílio Souza Costa Neto – FTC EAD
FONTE:http://obaricentrodamente.blogspot.com.br
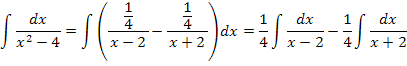
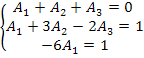
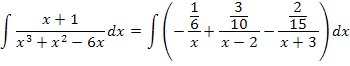
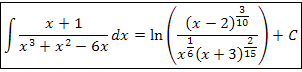
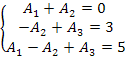
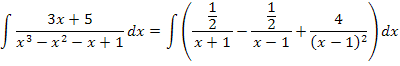
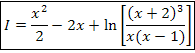
Nenhum comentário:
Postar um comentário