Potências de i

Marcelo Rigonatto

Números complexos

Os números complexos são pares ordenados de números reais (a, b) que escritos na forma normal são do tipo a + bi. O termo bi é chamado de parte imaginária e a de parte real. Sabemos que i² = – 1, mas como obter outras potências de i, como i¹⁵?

Vamos observar o comportamento presente nas potências de i e determinar um padrão que será utilizado para obter qualquer potência desse número. Para isso iremos recorrer a algumas propriedades da potenciação a fim de obter certas regularidades.

Sabemos que:

Observe que na potência de i com expoente 4 os valores começam a se repetir e o mesmo acontece nas potências com expoentes 8 e 12, caracterizando um padrão de repetição no cálculo dessas potências. Como os valores se repetem a cada quatro potências calculadas, ou seja, de 4 em 4, podemos obter o valor de qualquer potência de i utilizando o seguinte método:

Por exemplo, se desejamos calcular o valor de i¹²⁵.

Faremos a divisão de 125 por 4:

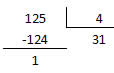
Calcular o valor de i¹²⁵ é o mesmo que calcular o valor de i elevado ao resto da divisão de 125 por 4, ou seja, é o mesmo que calcular i¹.

Assim,

i¹²⁵ = i¹ = i

Exemplo. Calcule o valor de i¹⁰²⁴.
Solução: Devemos fazer a divisão de 1024 por 4.


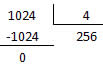
Assim, temos que:

i¹⁰²⁴ = i⁰ = 1.